
分析 (Ⅰ)当b=1时,把f(x)用分段函数来表示,分类讨论,求得f(x)≥1的解集.
(Ⅱ)当x∈R时,先求得f(x)的最大值为b2+1,再求得g(x)的最小值,根据g(x)的最小值减去f(x)的最大值大于或等于零,可得f(x)≤g(x)成立.
解答 解:(Ⅰ)由题意,当b=1时,f(x)=|x+b2|-|-x+1|=$\left\{\begin{array}{l}{-2,x≤-1}\\{2x,-1<x<1}\\{2,x≥1}\end{array}\right.$,
当x≤-1时,f(x)=-2<1,不等式f(x)≥1无解,不等式f(x)≥1的解集为∅;
当-1<x<1时,f(x)=2x,由不等式f(x)≥1,解得x≥$\frac{1}{2}$,所以$\frac{1}{2}$≤x<1;
当x≥1时,f(x)=2≥1恒成立,
所以不等式f(x)≥1的解集为[$\frac{1}{2}$,+∞).
(Ⅱ)(Ⅱ)当x∈R时,f(x)=|x+b2|-|-x+1|≤|x+b2 +(-x+1)|=|b2+1|=b2+1;
g(x)=|x+a2+c2|+|x-2b2|=≥|x+a2+c2-(x-2b2)|=|a2+c2+2b2|=a2+c2+2b2.
而 a2+c2+2b2-(b2+1)=a2+c2+b2-1=$\frac{1}{2}$( a2+c2+b2+a2+c2+b2 )-1≥ab+bc+ac-1=0,
当且仅当a=b=c=$\frac{\sqrt{3}}{3}$时,等号成立,即 a2+c2+2b2≥b2+1,即f(x)≤g(x).
点评 本题主要考查带有绝对值的函数,绝对值三角不等式的应用,比较2个数大小的方法,属于中档题.


 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案科目:高中数学 来源: 题型:解答题
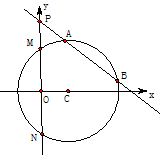 已知圆心在x轴正半轴上的圆C与直线5x+12y+21=0相切,与y轴交于M,N两点,且∠MCN=120°.
已知圆心在x轴正半轴上的圆C与直线5x+12y+21=0相切,与y轴交于M,N两点,且∠MCN=120°.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{6}{5}$ | B. | 1 | C. | $\frac{4}{5}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 数学成绩 | 90 | 97 | 105 | 113 | 127 | 130 | 135 |
| 物理成绩 | 105 | 116 | 120 | 127 | 135 | 130 | 140 |

查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com