
(本小题满分12分)已知圆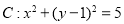 ,直线
,直线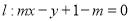
(1) 求证:对 ,直线
,直线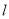 与圆
与圆 总有两个不同的交点A、B;
总有两个不同的交点A、B;
(2) 求弦AB的中点M的轨迹方程,并说明其轨迹是什么曲线;
(3) 若定点P(1,1)满足 ,求直线
,求直线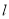 的方程。
的方程。
(1)证明见解析;(2)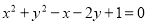 ,为圆的轨迹方程;(3)
,为圆的轨迹方程;(3)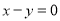 或
或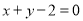 ;
;
【解析】
试题分析:(1)由题可知,判断直线与圆的位置关系,我们常采取两种方法,圆心到直线的距离与半径的比较,若距离大于半径,则位置关系是相离,若距离等于半径,则位置关系是相切,若距离小于半径,则位置关系是相交;或是判断直线所经过的定点和圆的关系,点在圆内,则位置关系是相交,点在圆上,则位置关系是相切,点在圆外,则位置关系是相离;(2)关于求轨迹方程的问题,求哪个点的轨迹就设哪个点的坐标,通过题中的条件将x,y的关系式求出,即得轨迹方程;(3)过一点的直线用点斜式设出,再和圆的方程联立,由韦达定理以及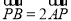 ,得出直线方程为
,得出直线方程为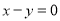 或
或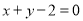 ;
;
试题解析:(Ⅰ)解法一:圆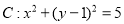 的圆心为
的圆心为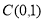 ,半径为
,半径为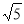 。
。
∴圆心C到直线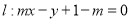 的距离
的距离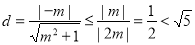 ,∴直线
,∴直线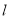 与圆C相交,即直线
与圆C相交,即直线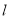 与圆C总有两个不同交点;
与圆C总有两个不同交点;
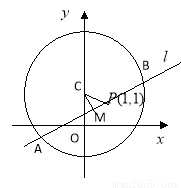
方法二:∵直线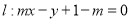 过定点
过定点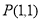 ,而点
,而点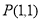 在圆内∴直线
在圆内∴直线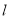 与圆C相交,即直线
与圆C相交,即直线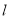 与圆C总有两个不同交点;(4分)
与圆C总有两个不同交点;(4分)
(Ⅱ)当M与P不重合时,连结CM、CP,则 ,又因为
,又因为
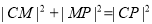 ,
,
设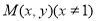 ,则
,则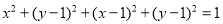 ,
,
化简得: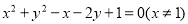
当M与P重合时,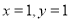 也满足上式。
也满足上式。
故弦AB中点的轨迹方程是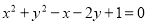 。(8分)
。(8分)
(Ⅲ)设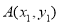 ,
,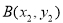 ,由
,由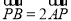 ,
,
∴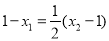 ,化简的
,化简的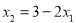 ①
①
又由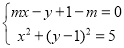 消去y得
消去y得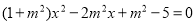 (*)
(*)
∴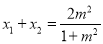 ② (10分)
② (10分)
由①②解得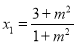 ,带入(*)式解得
,带入(*)式解得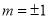 ,
,
∴直线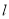 的方程为
的方程为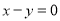 或
或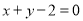 。(12分)
。(12分)
考点:?直线与圆的位置关系?中点轨迹方程?直线方程的应用


科目:高中数学 来源:2014-2015学年湖北省荆门市高三元月调研考试理科数学试卷(解析版) 题型:解答题
(本小题满分12分)如图,在四棱锥 中,底面
中,底面 是正方形,
是正方形, 底面
底面 ,
, , 点
, 点 是
是 的中点,
的中点, ,且交
,且交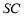 于点
于点 .
.

(Ⅰ)求证: 平面
平面 ;
;
(Ⅱ)求证:平面 ⊥平面
⊥平面 ;
;
(Ⅲ)求二面角 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年北京市东城区高三上学期期末教学统一检测理科数学试卷(解析版) 题型:选择题
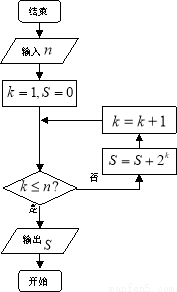
当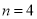 时,执行如图所示的程序框图,输出的
时,执行如图所示的程序框图,输出的 值为
值为
(A) (B)
(B)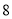 (C)
(C)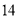 (D)
(D)
查看答案和解析>>
科目:高中数学 来源:2014-2015学年浙江省高二上学期期中考试文科数学试卷(解析版) 题型:选择题
点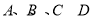 在同一个球的球面上,
在同一个球的球面上, ,若四面体
,若四面体 体积的最大值为
体积的最大值为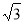 ,则这个球的表面积为( )
,则这个球的表面积为( )
A.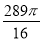 B.
B.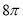 C.
C.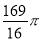 D.
D.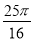
查看答案和解析>>
科目:高中数学 来源:2014-2015学年浙江省高二上学期期中考试文科数学试卷(解析版) 题型:选择题
已知二面角α-l-β的大小为60°,m,n为异面直线,且m⊥α,n⊥β,则m,n所成的角为( )
A.30° B.60° C.90° D.120°
查看答案和解析>>
科目:高中数学 来源:2014-2015学年浙江省高二上学期期中考试理科数学试卷(解析版) 题型:填空题
过点A(0,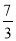 ),B(7,0)的直线l1与过(2,1),(3,k+1)的直线l2和两坐标轴围成的四边形内接于一个圆,则实数k的值为________.
),B(7,0)的直线l1与过(2,1),(3,k+1)的直线l2和两坐标轴围成的四边形内接于一个圆,则实数k的值为________.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年浙江省高二上学期期中考试理科数学试卷(解析版) 题型:选择题
如图所示是正方体的平面展开图.在这个正方体中,①BM与ED平行;②CN与BE是异面直线;③CN与BM成60°角;④DM与BN是异面直线.以上四个命题中,正确命题的序号是( )

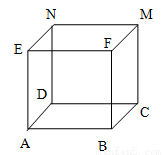
A.①②③ B.②④ C.③④ D.②③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com