
分析 (1)设数列{an}的公差为d,由题意和等差数列的通项公式列出方程组,求出a1和d,代入等差数列的通项公式求出an;
(2)由(1)和等差数列的前n项和公式求出Sn,利用配方法化简后,由二次函数的性质求出Sn的最大值;
(3)由(1)化简bn,利用裂项相消法求出前n项的和Tn.
解答 解:(1)设数列{an}的公差为d,…(1分)
由已知条件得,$\left\{\begin{array}{l}{{a}_{1}+d=1}\\{{a}_{1}+4d=-5}\end{array}\right.$,…(2分)
解得$\left\{\begin{array}{l}{{a}_{1}=3}\\{d=-2}\end{array}\right.$ …(3分)
所以an=3+(n-1)•(-2)=-2n+5;…(4分)
(2)由(1)得,Sn=$\frac{n({a}_{1}+{a}_{n})}{2}$=$\frac{n(3-2n+5)}{2}$
=-n2+4n=-(n-2)2+4.…(6分)
所以当n=2时,Sn取到最大值是4; …(8分)
(3)由(1)得,bn=$\frac{1}{(4-{a}_{n})(4-{a}_{n+1})}$=$\frac{1}{(2n-1)(2n+1)}$
=$\frac{1}{2}$($\frac{1}{2n-1}-\frac{1}{2n+1}$),…(10分)
所以Tn=b1+b2+…+bn-1+bn
=$\frac{1}{2}[(1-\frac{1}{3})+(\frac{1}{3}-\frac{1}{5})+…+(\frac{1}{2n-3}-\frac{1}{2n-1})+(\frac{1}{2n-1}-\frac{1}{2n+1})]$
=$\frac{1}{2}(1-\frac{1}{2n+1})=\frac{n}{2n+1}$----(12分)
点评 本题考查等差数列的通项公式,等差数列的前n项和公式以及最值问题,以及裂项相消法求数列的和,考查方程思想,化简、变形能力.


 名师点拨卷系列答案
名师点拨卷系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [2,68] | B. | [4,68] | C. | [2,2$\sqrt{17}$] | D. | [$\sqrt{2}$,2$\sqrt{17}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
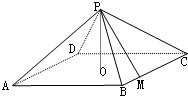 如图:四棱锥P-ABCD中,底面是以O为中心的菱形,PO⊥底面ABCD,AB=2,∠BAD=$\frac{π}{3}$,M是BC上的点,且BM=$\frac{1}{2}$,
如图:四棱锥P-ABCD中,底面是以O为中心的菱形,PO⊥底面ABCD,AB=2,∠BAD=$\frac{π}{3}$,M是BC上的点,且BM=$\frac{1}{2}$,查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com