
分析 利用抛物线得焦点弦公式,表示∴|PQ|=λ+$\frac{1}{λ}$+2,λ∈[$\frac{1}{2},2]$,再求其值域即可.
解答 解:(1)当λ=1时,PQ为抛物线得通经2p,|PQ|=4PQ=4;…(4分)
(2)由$\left\{\begin{array}{l}{{y}^{2}=4x}\\{x=ty+1}\end{array}\right.$得y2-4ty-4=0'
y1+y2=4t…①y1y2=-4…②
∵$\overrightarrow{PF}=λ\overrightarrow{PQ}$⇒y1=-λy2…③
由①②③消去y1,y2得4t2=λ+$\frac{1}{λ}$-2…④
∵直线L:x=ty+1过抛物线y2=4x的焦点为F(1,0),
∴|PQ|=x1+x2+2=t(y1+y2)+4=4t2+4…⑤.
把④代入⑤得∴|PQ|=λ+$\frac{1}{λ}$+2,λ∈[$\frac{1}{2},2]$
∴∴|PQ|$∈[4,\frac{9}{2}]$.
点评 本题考查了抛物线的焦点弦问题,焦点弦公式是关键.


科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | 0 | C. | 1 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 18 | B. | 12 | C. | 7 | D. | 24 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{3}}{2}$ | B. | -$\frac{\sqrt{3}}{2}$ | C. | $\frac{1}{2}$ | D. | -$\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
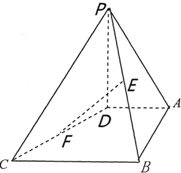 如图,在四棱锥P-ABCD中,PD⊥平面ABCD,AD∥BC,CD=13,AB=12,BC=10,AD=5,PD=8,点E,F分别是PB,DC的中点.
如图,在四棱锥P-ABCD中,PD⊥平面ABCD,AD∥BC,CD=13,AB=12,BC=10,AD=5,PD=8,点E,F分别是PB,DC的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com