考点:数列的求和
专题:等差数列与等比数列
分析:利用x1=1,x2=m(m≤1,m≠0),xn+2=|xn+1-xn|(n∈N*).可得x3=|x2-x1|=1-m.x4=|x3-x2|=|1-2m|,再利用周期为3可得x4=x1,m≠0,于是2m-1=1,解得m,可得x1+x2+x3=1+m+1-m=2.再利用周期性可求数列{xn}的前2014项的和S2014.
解答:
解:∵x1=1,x2=m(m≤1,m≠0),xn+2=|xn+1-xn|,
∴x3=|m-1|,又数列{xn}的周期为3,
∴x4=|x3-x2|=||m-1|-m|=x1=1,
解得:m=1或m=0,
∵m≠0,∴m=1,
∴x1=1,x2=1,x3=0;
即x1+x2+x3=2;
同理可得,x4=1,x5=1,x6=0,
x4+x5+x6=2;
…
x2011+x2012+x2013=2;
又x2014=x1=1,2014=671×3+1,
∴S2014=x1+x2+x3+…+x2014
=671×(1+1+0)+1
=1343.
故答案为:1343.
点评:本题考查数列的求和,着重考查函数的周期性,得到相邻三项之和为2是关键,属于中档题.



 阅读快车系列答案
阅读快车系列答案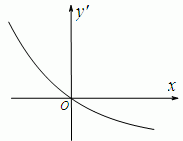 已知函数y=f(x)的导函数f′(x)的图象大致为如图,且f(15)=
已知函数y=f(x)的导函数f′(x)的图象大致为如图,且f(15)=