【题目】用系统抽样法从200名职工中抽取容量为20的样本，将200名职工从1至200编号，按编号顺序平均分成20组（1～10号，11～20号，…，191…200号），若第15组中抽出的号码为147，则第一组中按此抽签方法确定的号码是__________．
黄冈小状元解决问题天天练系列答案科目：高中数学 来源： 题型：
【题目】执行如图的程序框图，当n≥2，n∈Z时，fn（x）表示fn﹣1（x）的导函数，若输入函数f1（x）=sinx﹣cosx，则输出的函数fn（x）可化为（ ）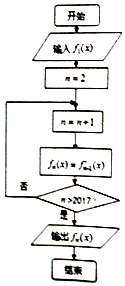 
A.
sin（x+ 
）
B. sin（x﹣ ）??
C.﹣ sin（x+ ）
D.﹣ sin（x﹣ ）
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】空气质量指数（Air Quality Index，简称AQI）是定量描述空气质量状况的质量状况的指数，空气质量按照AQI大小分为六级，0～50为优；51～100为良101﹣150为轻度污染；151﹣200为中度污染；201～300为重度污染；＞300为严重污染． 一环保人士记录去年某地某月10天的AQI的茎叶图如图．
（Ⅰ）利用该样本估计该地本月空气质量优良（AQI≤100）的天数；（按这个月总共30天）
（Ⅱ）将频率视为概率，从本月中随机抽取3天，记空气质量优良的天数为ξ，求ξ的概率分布列和数学期望．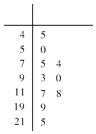
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某学校为了分析在一次数学竞赛中甲、乙两个班的数学成绩，分别从甲、乙两个班中随机抽取了10个学生的成绩，成绩的茎叶图如下：
（Ⅰ）根据茎叶图，计算甲班被抽取学生成绩的平均值
及方差
；
（Ⅱ）若规定成绩不低于90分的等级为优秀，现从甲、乙两个班级所抽取成绩等级为优秀的学生中，随机抽取2人，求这两个人恰好都来自甲班的概率.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数f（x）=|x﹣m|﹣|x+3m|（m＞0）． （Ⅰ）当m=1时，求不等式f（x）≥1的解集；
（Ⅱ）对于任意实数x，t，不等式f（x）＜|2+t|+|t﹣1|恒成立，求m的取值范围．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数
在
上是增函数，则
的取值范围是（ ）
A. 
B. 
C. 
D. 
【答案】C
【解析】
若函数f（x）=log2（x2﹣ax+3a）在[2，+∞）上是增函数，则x2﹣ax+3a＞0且f（2）＞0，根据二次函数的单调性，我们可得到关于a的不等式，解不等式即可得到a的取值范围．
若函数f（x）=log2（x2﹣ax+3a）在[2，+∞）上是增函数，
则当x∈[2，+∞）时，
x2﹣ax+3a＞0且函数f（x）=x2﹣ax+3a为增函数
即
，f（2）=4+a＞0
解得﹣4＜a≤4
故选：C．
【点睛】
本题考查的知识点是复合函数的单调性，二次函数的性质，对数函数的单调区间，其中根据复合函数的单调性，构造关于a的不等式，是解答本题的关键．
【题型】单选题
【结束】
10
【题目】圆锥的高
和底面半径
之比
，且圆锥的体积
，则圆锥的表面积为（ ）
A. 
B. 
C. 
D. 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
