Question

【题目】已知三棱柱的侧棱垂直于底面，，，，，分别是，的中点.

（Ⅰ）证明：平面；

（Ⅱ）求二面角的余弦值.

Answer 1

【答案】(1)见解析;(2).

【解析】分析：解法一：依题意可知两两垂直，以点为原点建立空间直角坐标系，

（1）利用直线的方向向量和平面的法向量垂直，即可证得线面平面；

（2）求出两个平面的法向量，利用两个向量的夹角公式，即可求解二面角的余弦值.

解法二：利用空间几何体的点线面位置关系的判定定理和二面角的定义求解：

（1）设的中点为，连接，证明四边形为平行四边形，得出线线平行，利用线面平行的判定定理即可证得线面平面；

（2）以及二面角的平面角，在直角三角形中求出其平面角的余弦值，即可得到二面角的余弦值.

详解：解法一：依条件可知、、两两垂直，

如图，以点为原点建立空间直角坐标系.

根据条件容易求出如下各点坐标：，，，，，，，.

（Ⅰ）证明：∵，，

是平面的一个法向量，且，

所以.

又∵平面，∴平面；

（Ⅱ）设是平面的法向量，

因为，，

由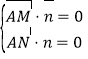，得.

解得平面的一个法向量，

由已知，平面的一个法向量为，

，

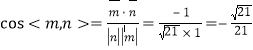∴二面角的余弦值是.

解法二：

（Ⅰ）证明：设的中点为，连接，，

∵，分别是，的中点，∴，

又∵，，

∴，∴四边形是平行四边形，

∴，∵平面，平面，

∴平面；

（Ⅱ）如图，设的中点为，连接，

∴，∵底面，∵，，∴，，

∴，∴底面，

在平面内，过点做，垂足为，

连接，，，，

∴平面，则，

∴是二面角的平面角，

∵，由，得，

所以，所以，

∴二面角的余弦值是.