
【题目】已知函数![]() ,
,![]() .
.
(1)求函数![]() 的最小正周期;
的最小正周期;
(2)若存在![]() ,使不等式
,使不等式![]() 成立,求实数
成立,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]()
![]()
![]()
![]() ……………………4分
……………………4分
∴ 函数f(x)的最小正周期![]() ……………………6分
……………………6分
(2)当![]() 时,
时,![]()
∴ 当![]() ,即
,即![]() 时,f(x)取最小值-1 ………9分
时,f(x)取最小值-1 ………9分
所以使题设成立的充要条件是![]() ,
,
故m的取值范围是(-1,+∞) ………10分
【解析】
(Ⅰ)利用三角函数的恒等变换化简函数f(x)的解析式为2sin(2x+![]() ),从而求出它的最小正周期.(Ⅱ)根据
),从而求出它的最小正周期.(Ⅱ)根据![]() ,可得 sin(2x0+
,可得 sin(2x0+![]() )∈[﹣
)∈[﹣![]() ,1],f(x0)的值域为[﹣1,2],若存在
,1],f(x0)的值域为[﹣1,2],若存在![]() 使不等式f(x0)<m成立,m需大于f(x0)的最小值.
使不等式f(x0)<m成立,m需大于f(x0)的最小值.
(Ⅰ)∵![]()
=[2sinx+![]() cosx]cosx﹣
cosx]cosx﹣![]() =sin2x+
=sin2x+![]() ﹣
﹣![]() +
+![]() cos2x
cos2x
=sin2x+![]() cos2x=2sin(2x+
cos2x=2sin(2x+)
∴函数f(x)的最小周期T=![]() .
.
(Ⅱ)∵![]() ,∴2x0+
,∴2x0+![]() ∈[
∈[![]() ,
,![]() ],∴sin(2x0+
],∴sin(2x0+![]() )∈[﹣
)∈[﹣![]() ,1],
,1],
∴f(x0)的值域为[﹣1,2].
∵存在![]() ,使f(x)<m成立,∴m>﹣1,
,使f(x)<m成立,∴m>﹣1,
故实数m的取值范围为(﹣1,+∞).


科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,曲线C的参数方程为 ![]() (α为参数).以坐标原点O为极点,x轴正半轴为极轴建立极坐标系,直线l的极坐标方程为ρcos(θ+
(α为参数).以坐标原点O为极点,x轴正半轴为极轴建立极坐标系,直线l的极坐标方程为ρcos(θ+ ![]() )=
)= ![]() .l与C交于A、B两点. (Ⅰ)求曲线C的普通方程及直线l的直角坐标方程;
.l与C交于A、B两点. (Ⅰ)求曲线C的普通方程及直线l的直角坐标方程;
(Ⅱ)设点P(0,﹣2),求|PA|+|PB|的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校为了分析在一次数学竞赛中甲、乙两个班的数学成绩,分别从甲、乙两个班中随机抽取了10个学生的成绩,成绩的茎叶图如下:

(Ⅰ)根据茎叶图,计算甲班被抽取学生成绩的平均值![]() 及方差
及方差![]() ;
;
(Ⅱ)若规定成绩不低于90分的等级为优秀,现从甲、乙两个班级所抽取成绩等级为优秀的学生中,随机抽取2人,求这两个人恰好都来自甲班的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知正项数列![]() 的前
的前![]() 项和为
项和为![]() ,满足
,满足![]() .
.
(Ⅰ)(i)求数列![]() 的通项公式;
的通项公式;
(ii)已知对于![]() ,不等式
,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的最小值;
的最小值;
(Ⅱ) 数列![]() 的前
的前![]() 项和为
项和为![]() ,满足
,满足![]() ,是否存在非零实数
,是否存在非零实数![]() ,使得数列
,使得数列![]() 为等比数列? 并说明理由.
为等比数列? 并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,底面ABCD是菱形,且∠DAB=60°.点E是棱PC的中点,平面ABE与棱PD交于点F. (Ⅰ)求证:AB∥EF;
(Ⅱ)若PA=PD=AD,且平面PAD⊥平面ABCD,求平面PAF与平面AFE所成的锐二面角的余弦值.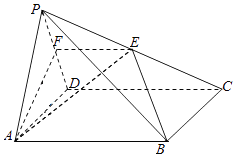
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】命题p:f(x)=-x2+2ax+1-a在x∈[0,1]时的最大值不超过2,命题q:正数x,y满足x+2y=8,且![]() 恒成立. 若p∨(q)为假命题,求实数a的取值范围.
恒成立. 若p∨(q)为假命题,求实数a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com