
分析 可先求出向量$\overrightarrow{a}-2\overrightarrow{b}$的坐标,根据条件得到$(\overrightarrow{a}-2\overrightarrow{b})•\overrightarrow{a}=0$,从而可求出x=1,进而求出向量$\overrightarrow{a}-2\overrightarrow{b}$的坐标,从而求得该向量的长度.
解答 解:∵$\overrightarrow{a}-2\overrightarrow{b}=(-1,2-x)$,且$(\overrightarrow{a}-2\overrightarrow{b})⊥\overrightarrow{a}$;
∴$(\overrightarrow{a}-2\overrightarrow{b})•\overrightarrow{a}=-1+x(2-x)$=-x2+2x-1=0;
∴x=1;
∴$\overrightarrow{a}-2\overrightarrow{b}=(-1,1)$;
∴$|\overrightarrow{a}-2\overrightarrow{b}|=\sqrt{2}$.
故答案为:$\sqrt{2}$.
点评 考查向量坐标的概念,向量垂直的充要条件,以及向量坐标的数乘运算.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{1}{3}$ | D. | $\frac{3}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
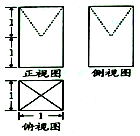
| A. | 2 | B. | $\frac{2}{3}$ | C. | $\frac{4}{3}$ | D. | $\frac{5}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | “?x∈R,ex>0”的否定是“?x∈R,使ex>0” | |
| B. | 若x+y≠3(x,y∈R),则x≠2或y≠1 | |
| C. | “x2+2x≥ax(1≤x≤2)恒成立”等价于“(x2+2x)min≥(ax)max(1≤x≤2)” | |
| D. | “若a=-1,则函数f(x)=ax2+2x-1只有一个零点”的逆命题为真命题 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2i | B. | 0 | C. | 2i | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{5}{9}$ | B. | $\frac{4}{9}$ | C. | $\frac{3}{5}$ | D. | $\frac{2}{5}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com