
| A. | $\sqrt{3}$ | B. | $\frac{3}{2}$ | C. | $\frac{9}{4}$ | D. | 9 |
分析 在△ABC中,由余弦定理求得BC,得到OB,再由正弦定理求得sinB,结合平方关系求得cosB,然后在△AOB中由余弦定理得答案.
解答 解:如图, ∵∠A=120°,AC=$\sqrt{3}$,AB=2$\sqrt{3}$,
∵∠A=120°,AC=$\sqrt{3}$,AB=2$\sqrt{3}$,
∴$BC=\sqrt{A{B}^{2}+A{C}^{2}-2AB•AC•cos∠BAC}$=$\sqrt{(2\sqrt{3})^{2}+(\sqrt{3})^{2}-2×2\sqrt{3}×\sqrt{3}×(-\frac{1}{2})}$=$\sqrt{21}$.
∴OB=$\frac{\sqrt{21}}{2}$.
又$\frac{AC}{sinB}=\frac{BC}{sinA}$,得$\frac{\sqrt{3}}{sinB}=\frac{\sqrt{21}}{sin120°}$,∴sinB=$\frac{\sqrt{21}}{14}$,则cosB=$\frac{5\sqrt{7}}{14}$.
则AO=$\sqrt{A{B}^{2}+O{B}^{2}-2AB•OB•cosB}$=$\sqrt{(2\sqrt{3})^{2}+(\frac{\sqrt{21}}{2})^{2}-2×2\sqrt{3}×\frac{\sqrt{21}}{2}×\frac{5\sqrt{7}}{14}}$=$\frac{3}{2}$.
故选:B.
点评 本题考查正弦定理和余弦定理在解三角形中的应用,考查计算能力,属中档题.


 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案科目:高中数学 来源: 题型:选择题
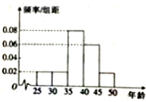 2015年某企业员工有500人参加“学雷锋”志愿活动,按年龄分组:第1组[25,30),第2组[30,35),第3组[35,40),第4组[40,45),第5组[45,50),得到的频率分布直方图如图所示.现在要从年龄较小的第1,3,4组中用分层抽样的方法抽取16人,则在第4组抽取的人数为( )
2015年某企业员工有500人参加“学雷锋”志愿活动,按年龄分组:第1组[25,30),第2组[30,35),第3组[35,40),第4组[40,45),第5组[45,50),得到的频率分布直方图如图所示.现在要从年龄较小的第1,3,4组中用分层抽样的方法抽取16人,则在第4组抽取的人数为( )| A. | 3 | B. | 6 | C. | 4 | D. | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 圆 | B. | 抛物线 | C. | 椭圆 | D. | 双曲线 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
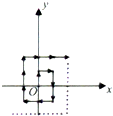 如图所示,质点A从坐标原点O开始沿箭头所指方向作规则运动,每次只运动一个单位,相应的质点的坐标记为An,如A1(0,1),A2(1,1),A3(1,0),A4(1,-1),…,则A2015的坐标为( )
如图所示,质点A从坐标原点O开始沿箭头所指方向作规则运动,每次只运动一个单位,相应的质点的坐标记为An,如A1(0,1),A2(1,1),A3(1,0),A4(1,-1),…,则A2015的坐标为( )| A. | (-21,12) | B. | (-22,12) | C. | (-21,13) | D. | (-22,13) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | $\frac{5}{2}\sqrt{21}$ | B. | $\frac{25}{4}$ | C. | $\frac{15}{4}$ | D. | $\frac{3}{2}\sqrt{5}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com