
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
分析 由i2=-1化简复数z,然后求出Z的共轭复数在复平面中对应的点的坐标,则答案可求.
解答 解:由复数(1-i2015)•Z=i2014,
得$z=\frac{{i}^{2014}}{1-{i}^{2015}}=\frac{({i}^{2})^{1007}}{1-({i}^{2})^{1007}•i}=\frac{-1}{1+i}$=$-\frac{1-i}{(1+i)(1-i)}=-\frac{1-i}{2}=-\frac{1}{2}+\frac{1}{2}i$.
则$\overline{z}$=$-\frac{1}{2}-\frac{1}{2}i$.
∴Z的共轭复数在复平面中对应的点的坐标为:($-\frac{1}{2}$,$-\frac{1}{2}$).
位于第三象限.
故选:C.
点评 本题考查了复数的基本概念,考查了复数的代数表示法及其几何意义,是基础题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
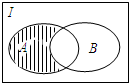
| A. | {-1,0,1} | B. | {2,3} | C. | {-2,2,3} | D. | {-1,0,1,2,3} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
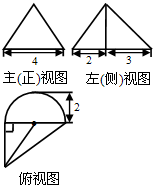 一个几何体的三视图如图所示,其主(正)视图是一个等边三角形,则这个几何体的体积为( )
一个几何体的三视图如图所示,其主(正)视图是一个等边三角形,则这个几何体的体积为( )| A. | $12\sqrt{3}+4\sqrt{3}π$ | B. | $\frac{{4\sqrt{39}}}{3}+\frac{{4\sqrt{3}π}}{3}$ | C. | $12\sqrt{3}+\frac{{4\sqrt{3}π}}{3}$ | D. | $4\sqrt{3}+\frac{{4\sqrt{3}π}}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com