练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    本公司计划在甲、乙两个电视台做总时间不超过300min的广告,广告总费用不超过9万元.甲、乙电视台的广告收费标准分别为500元/分钟和200元/分钟.假定甲、乙两个电视台为该公司所做的每分钟广告,能给公司带来的收益分别为0.3万元和0.2万元.问:该公司如何分配在甲、乙两个电视台的广告时间,才能使公司的收益最大?最大收益是多少万元?


     设公司在甲电视台和乙电视台做广告的时间分别为xmin和ymin,总收益为z元.

    由题意得目标函数为z=3 000x+2 000y.

    二元一次不等式组等价于

    作出二元一次不等式组所表示的可行域.

    如图,作直线l:3 000x+2 000y=0,即3x+2y=0,平移直线l,

    从图中可知,当直线l过点M时,目标函数取得最大值.

    联立解得x=100,y=200.

    所以点M的坐标为(100,200).

    所以zmax=3 000x+2 000y=700 000(元).

    答:该公司在甲电视台做100min广告,在乙电视台做200min广告,公司的收益最大.最大收益是70万元.


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    设m,n∈N*,f(x)=(1+x)m+(1+x)n.

    (1) 当m=n=7时,f(x)=a7x7+a6x6+…+a1x+a0,求a0+a2+a4+a6的值;

    (2) 当m=n时,f(x)展开式中x2的系数是20,求n的值;

    (3) 若f(x)展开式中x的系数是19,当m,n变化时,求x2系数的最小值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设A=,B=,X=,试解方程AX=B.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


     中心在原点、焦点在x轴上的椭圆C的焦距为2,两准线间的距离为10.设点A(5,0),过点A作直线l交椭圆C于P,Q两点,过点P作x轴的垂线交椭圆C于另一点S.

    (1) 求椭圆C的方程;

    (2) 求证:直线SQ过x轴上一定点B;

    (3) 若过点A作直线与椭圆C只有一个公共点D,求过B,D两点、且以AD为切线的圆的方程.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知实数x,y满足那么z=·的最小值为　　　　. 

    查看答案和解析>>

    科目：高中数学 来源： 题型：


     设向量a=(cosα,sinα),b=(cosβ,sinβ),其中0<α<β<π,若|2a+b|=|a-2b|,则β-α=　　　　. 

    查看答案和解析>>

    科目：高中数学 来源： 题型：


     已知向量a=(cosωx+sinωx,sinωx),b=(-cosωx+sinωx,2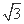cosωx),设函数f(x)=a·b+λ(x∈R)的图象关于直线x=π对称,其中ω,λ为常数,且ω∈.

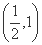    (1) 求函数f(x)的最小正周期;

    (2) 若函数f(x)的图象经过点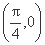,求函数f(x)在区间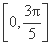上的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知一船以15 km/h的速度向东航行,船在A处看到一个灯塔M在北偏东60°方向,行驶4 h后,船到达B处,看到这个灯塔在北偏东15°方向,这时船与灯塔的距离为　　　　km. 

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知数列{an}的前n项和为Sn,且点(n,Sn)在函数y=2x+1-2的图象上.

    (1) 求数列{an}的通项公式;

    (2) 设数列{bn}满足:b1=0,bn+1+bn=an(n∈N*),求数列{bn}的前n项和公式;

    (3) 在第(2)问的条件下,若对于任意的n∈N*,不等式bn<λbn+1恒成立,求实数λ的取值范围.

    查看答案和解析>>

    同步练习册答案