
已知向量a=(cosωx+sinωx,sinωx),b=(-cosωx+sinωx,2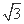 cosωx),设函数f(x)=a·b+λ(x∈R)的图象关于直线x=π对称,其中ω,λ为常数,且ω∈
cosωx),设函数f(x)=a·b+λ(x∈R)的图象关于直线x=π对称,其中ω,λ为常数,且ω∈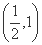 .
.
(1) 求函数f(x)的最小正周期;
(2) 若函数f(x)的图象经过点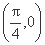 ,求函数f(x)在区间
,求函数f(x)在区间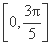 上的取值范围.
上的取值范围.
(1)因为f(x)=sin2 ωx-cos2 ωx+2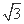 sin ωx·cos ωx+λ=-cos 2ωx+
sin ωx·cos ωx+λ=-cos 2ωx+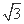 sin 2ωx+λ=2sin
sin 2ωx+λ=2sin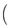 2ωx-
2ωx-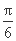
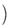 +λ.
+λ.
由直线x=π是函数f(x)图象的一条对称轴,
可得sin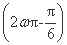 =±1,
=±1,
所以2ωπ-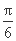 =kπ+
=kπ+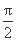 (k∈Z),
(k∈Z),
即ω=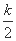 +
+ (k∈Z).
(k∈Z).
又ω∈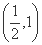 ,k∈Z,所以k=1,故ω=
,k∈Z,所以k=1,故ω=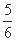 .
.
所以函数f(x)的最小正周期是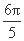 .
.
(2) 由函数f(x)的图象过点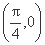 ,得f
,得f =0,
=0,
即λ=-2sin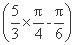 =-2sin
=-2sin  =-
=-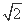 ,
,
即λ=-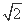 ,故f(x)=2sin
,故f(x)=2sin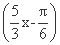 -
-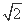 .
.
由0≤x≤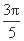 ,得-
,得-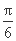 ≤
≤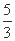 x-
x-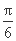 ≤
≤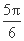 ,
,
所以-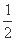 ≤sin
≤sin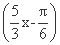 ≤1,
≤1,
所以-1-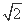 ≤f(x)≤2-
≤f(x)≤2-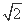 ,
,
故函数f(x)的取值范围为[-1-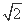 ,2-
,2-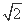 ].
].


科目:高中数学 来源: 题型:
已知双曲线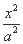 -
-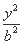 =1(a>0,b>0)的两个焦点为F1
=1(a>0,b>0)的两个焦点为F1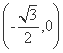 ,F2
,F2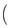
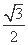 ,0
,0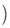 ,点P是第一象限内双曲线上的点,且tan∠PF1F2=
,点P是第一象限内双曲线上的点,且tan∠PF1F2=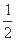 ,tan∠PF2F1=-2,则双曲线的离心率为 .
,tan∠PF2F1=-2,则双曲线的离心率为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
本公司计划在甲、乙两个电视台做总时间不超过300min的广告,广告总费用不超过9万元.甲、乙电视台的广告收费标准分别为500元/分钟和200元/分钟.假定甲、乙两个电视台为该公司所做的每分钟广告,能给公司带来的收益分别为0.3万元和0.2万元.问:该公司如何分配在甲、乙两个电视台的广告时间,才能使公司的收益最大?最大收益是多少万元?
查看答案和解析>>
科目:高中数学 来源: 题型:
在△ABC中,角A,B,C所对的边长分别为a,b,c,设向量x=(sinB,sinC),y=(cosB,cosC),z=(cosB,-cosC),若z∥(x+y),则tanB+tanC= .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com