练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    在平面直角坐标系xOy中,设点P为圆C:(x-1)2+y2=4上的任意一点,已知点Q(2a,a-3)(a∈R),则线段PQ长度的最小值为　　　　. 


    -2


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


     已知向量a=(cosωx+sinωx,sinωx),b=(-cosωx+sinωx,2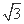cosωx),设函数f(x)=a·b+λ(x∈R)的图象关于直线x=π对称,其中ω,λ为常数,且ω∈.

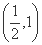    (1) 求函数f(x)的最小正周期;

    (2) 若函数f(x)的图象经过点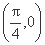,求函数f(x)在区间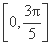上的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    现有如下命题:

    ①过平面外一点有且只有一条直线与该平面垂直;

    ②过平面外一点有且只有一条直线与该平面平行;

    ③如果两个平行平面和第三个平面相交, 那么所得的两条交线平行;

    ④如果两个平面相互垂直, 那么经过第一个平面内一点且垂直于第二个平面的直线必在第一个平面内.则所有真命题的序号是　　　　.(填序号) 

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知数列{an}的前n项和为Sn,且点(n,Sn)在函数y=2x+1-2的图象上.

    (1) 求数列{an}的通项公式;

    (2) 设数列{bn}满足:b1=0,bn+1+bn=an(n∈N*),求数列{bn}的前n项和公式;

    (3) 在第(2)问的条件下,若对于任意的n∈N*,不等式bn<λbn+1恒成立,求实数λ的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知正项数列{an}满足Sn=.

    (1) 求a1,a2,a3并推测an;

    (2) 用数学归纳法证明你的结论.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知圆x2+y2+2ax-2ay+2a2-4a=0(0<a≤4)的圆心为C,直线l:y=x+m.

    (1) 若m=4,求直线l被圆C所截得弦长的最大值;

    (2) 若直线l是圆心C下方的切线,当a在(0,4]上变化时,求m的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    在极坐标系中,圆C的方程为ρ=4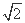cos,以极点为坐标原点、极轴为x轴的正半轴建立平面直角坐标系,直线l的参数方程为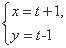(t为参数),求直线l被圆C截得的弦AB的长度.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


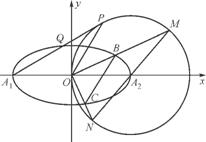
    如图,在平面直角坐标系xOy中,已知椭圆E: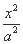+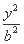=1(a>b>0)的离心率e=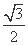,A1,A2分别是椭圆E的左、右两个顶点,圆A2的半径为a,过点A1作圆A2的切线,切点为P,在x轴的上方交椭圆E于点Q.

    (1) 求直线OP的方程;

    (2) 求的值;

    (3) 设a为常数,过点O作两条互相垂直的直线,分别交椭圆E于点B,C,分别交圆A2于点M,N,记OBC和OMN的面积分别为S1,S2,求S1·S2的最大值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知M＝{x|x2－5x＋6＝0}，N＝{x|ax＝12}，若N⊆M，求实数a所构成的集合A，并写出A的所有非空真子集.

    查看答案和解析>>

    同步练习册答案