练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    在△ABC中，已知A=60°，b=4，c=5，则sinB+sinC=    ．
    【答案】分析：由cosA，b及c的值，利用余弦定理求出a的值，然后由sinA，a，b及c的值分别求出sinB和sinC的值，即可求出sinB+sinC的值．
    解答：解：由A=60°，b=4，c=5，
    根据余弦定理a2=b2+c2-2bccosA得：
    a2=16+25-2×4×5×=21，
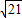
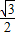
    解得：a=，又sinA=，b=4，c=5，
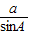
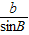
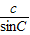
    根据正弦定理==得：
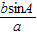
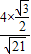
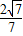
    sinB===，sinC===，
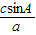
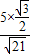
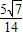
    则sinB+sinC=+=．
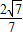
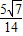
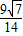
    故答案为：
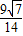    点评：此题考查了正弦定理，以及余弦定理．熟练掌握定理是解本题的关键．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    在△ABC中，已知A、B、C成等差数列，求tg（
    A
    2
    ）+
    		3
    tg（
    A
    2
    ）tg（
    C
    2
    ）+tg（
    C
    2
    ）的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    在△ABC中，已知A=45°，a=2，b=
    		2
    ，则B等于（　　）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    在△ABC中，已知a=
    		3
    ，b=
    		2
    ，1+2cos（B+C）=0，求：
    （1）角A，B； 
    （2）求BC边上的高．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    在△ABC中，已知A=60°，
    AB
    •
    AC
    =1，则△ABC的面积为
    		3
    2
    		3
    2
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    在△ABC中，已知a=1，b=2，cosC=
    34
    ．
    （1）求AB的长；
    （2）求sinA的值．

    查看答案和解析>>

    同步练习册答案