练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    执行如图所示的算法流程图，则最后输出的等于       ．


    63


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    甲、乙、丙、丁四位同学各自对A、B两变量的线性相关性做试验，并用回归分析方法分别求得相关系数r与残差平方和m如下表：

     

    甲

    乙

    丙

    丁

    r

    0.82

    0.78

    0.69

    0.85

    m

    115

    106

    124

    103

    则哪位同学的试验结果体现A、B两变量更强的线性相关性？　(　　)

    A．甲　　  B．乙　  C．丙　　　  D．丁

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知：圆C：x2＋y2－8y＋12＝0，直线l：ax＋y＋2a＝0.

    (1)当a为何值时，直线l与圆C相切；

    (2)当直线l与圆C相交于A、B两点，且AB＝2时，求直线l的方程．

     

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    用四个不同数字组成四位数,所有这些四位数中的数字的总和为,则=      。

    查看答案和解析>>

    科目：高中数学 来源： 题型：


        已知函数．

    （1）当时，求函数的单调区间；

    （2）若函数在处取得极值，对,恒成立，求实数的取值范围；

    （3）当时，求证：．

     

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设等差数列的前项和为，若，，，则正整数=   

    查看答案和解析>>

    科目：高中数学 来源： 题型：


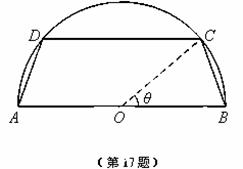
    一个圆柱形圆木的底面半径为1m，长为10m，将此圆木沿轴所在的平面剖成两个部分．现要把其中一个部分加工成直四棱柱木梁，长度保持不变，底面为等腰梯形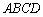（如图所示，其中O为圆心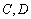，在半圆上），设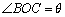，木梁的体积为V（单位：m3），表面积为S（单位：m2）．

    （1）求V关于θ的函数表达式；

    （2）求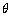的值，使体积V最大；

    （3）问当木梁的体积V最大时，其表面积S是否也最大？请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    函数的递增区间是(     )

    A.        B.和         C.      D.和

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知向量a，b满足，且，则的取值范围是

      (A)[4,5]          (B)[5,6]          (C)[3,6]           (D)

    查看答案和解析>>

    同步练习册答案