
已知焦点在y轴,顶点在原点的抛物线C1经过点P(2,2),以C1上一点C2为圆心的圆过定点A(0,1),记 为圆
为圆 与
与 轴的两个交点.
轴的两个交点.
(1)求抛物线 的方程;
的方程;
(2)当圆心 在抛物线上运动时,试判断
在抛物线上运动时,试判断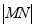 是否为一定值?请证明你的结论;
是否为一定值?请证明你的结论;
(3)当圆心 在抛物线上运动时,记
在抛物线上运动时,记 ,
, ,求
,求 的最大值.
的最大值.
(1)x2=2y ;(2)定值2;(3)
【解析】
试题分析:(1)由焦点在y轴,顶点在原点的抛物线假设为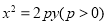 ,又C1经过点P(2,2),即可求出抛物线的
,又C1经过点P(2,2),即可求出抛物线的 .即可得抛物线的方程.
.即可得抛物线的方程.
(2)当圆心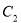 在抛物线上运动时,写出圆
在抛物线上运动时,写出圆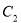 的方程,再令y=0即可求得圆的方程与x轴的两交点的坐标,计算两坐标的差即可得到结论.
的方程,再令y=0即可求得圆的方程与x轴的两交点的坐标,计算两坐标的差即可得到结论.
(3)当圆心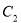 在抛物线上运动时,由(1)可得M,N的坐标(其中用圆心
在抛物线上运动时,由(1)可得M,N的坐标(其中用圆心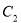 的坐标表示).根据两点的距离公式即可用圆心
的坐标表示).根据两点的距离公式即可用圆心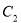 的坐标表示m,n的值,将
的坐标表示m,n的值,将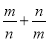 适当变形,再根据基本不等式即可求得
适当变形,再根据基本不等式即可求得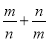 的最大值.
的最大值.
(1)由已知,设抛物线方程为x2=2py,22=2p×2,解得p=1.
所求抛物线C1的方程为x2=2y.-------3分
(2)法1:设圆心C2(a,a2/2),则圆C2的半径r=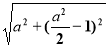
圆C2的方程为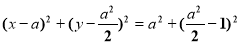 .
.
令y=0,得x2-2ax+a2-1=0,得x1=a-1,x2=a+1.
|MN|=|x1-x2|=2(定值).------7分
法2:设圆心C2(a,b),因为圆过A(0,1),所以半径r=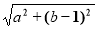 ,
,
,因为C2在抛物线上,a2=2b,且圆被x轴截得的弦长
|MN|=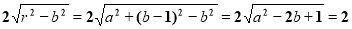 (定值)---7分
(定值)---7分
(3)由(2)知,不妨设M(a-1,0),N(a+1,0),

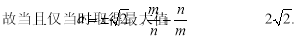
考点:1.抛物线的性质.2.最值问题.3.基本不等式的应用.


科目:高中数学 来源:2013-2014学年福建省龙岩市高三上学期期末考试文科数学试卷(解析版) 题型:选择题
已知直线2x-y+6=0过双曲线C: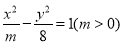 的一个焦点,则双曲线的离心率为( )
的一个焦点,则双曲线的离心率为( )
A、 B、2 C、3 D、4
B、2 C、3 D、4
查看答案和解析>>
科目:高中数学 来源:2013-2014学年福建省高三高考压轴文科数学试卷(解析版) 题型:选择题
如图给出的是计算 的值的一个程序框图,其中判断框内应填入的条件是( )
的值的一个程序框图,其中判断框内应填入的条件是( )
A. B.
B. C.
C. D.
D.

查看答案和解析>>
科目:高中数学 来源:2013-2014学年福建省福州市高三5月综合练习理科数学试卷(解析版) 题型:填空题
在集合 所表示的平面区域内任取一点M,则点M恰好取自
所表示的平面区域内任取一点M,则点M恰好取自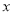 轴上方的概率为___ _____.
轴上方的概率为___ _____.

查看答案和解析>>
科目:高中数学 来源:2013-2014学年福建省福州市高三5月综合练习文科数学试卷(解析版) 题型:填空题
已知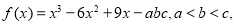 且
且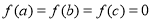 ,现给出如下结论:
,现给出如下结论:
①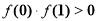 ;②
;② ;③
;③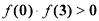 ;④;
;④;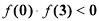 ;
;
⑤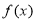 的极值为1和3.其中正确命题的序号为 .
的极值为1和3.其中正确命题的序号为 .
查看答案和解析>>
科目:高中数学 来源:2013-2014学年福建省福州市高三5月综合练习文科数学试卷(解析版) 题型:选择题
已知直线a,b异面, ,给出以下命题:①一定存在平行于a的平面
使 ;②一定存在平行于a的平面
;②一定存在平行于a的平面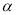 使
使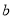 ∥
∥ ;③一定存在平行于a的平面
;③一定存在平行于a的平面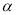 使
使 ;④一定存在无数个平行于a的平面
;④一定存在无数个平行于a的平面 与b交于一定点.则其中论断正确的是( )
与b交于一定点.则其中论断正确的是( )
A.①④ B.②③ C.①②③ D.②③④
查看答案和解析>>
科目:高中数学 来源:2013-2014学年福建省高考考前模拟理科数学试卷(解析版) 题型:填空题
已知集合 ,若对于任意实数对
,若对于任意实数对 ,存在
,存在 ,使得
,使得 成立,则称集合
成立,则称集合 为“正交点集”,给出下列集合:
为“正交点集”,给出下列集合:
① ;②
;② ;③
;③ ;
;
④ ;⑤
;⑤ .
.
则满足条件的“正交集合”有:_________________________(写出所有满足条件的集合的序号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com