
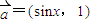 ,
,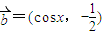 ,函数
,函数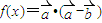 ,那么下列四个命题中正确命题的序号是 .
,那么下列四个命题中正确命题的序号是 .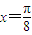 时,f(x)有最小值
时,f(x)有最小值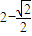 .
. π,-
π,- π]是函数f(x)的一个单调递增区间;
π]是函数f(x)的一个单调递增区间;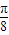 ,2)是函数f(x)的一个对称中心.
,2)是函数f(x)的一个对称中心. 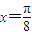 时,
时,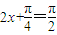 ,所以
,所以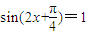 ,可得f(x)有最小值
,可得f(x)有最小值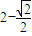 ;
; π,-
π,- π]时,
π]时,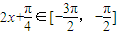 ,可得[-
,可得[- π,-
π,- π]是函数f(x)的一个单调递增区间;
π]是函数f(x)的一个单调递增区间; ,0)是函数g(x)=
,0)是函数g(x)=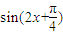 的一个对称中心,可得结论.
的一个对称中心,可得结论.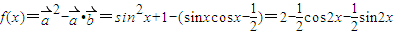 =
=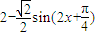 ,∴①f(x)是周期函数,其最小正周期为π,故①错;
,∴①f(x)是周期函数,其最小正周期为π,故①错;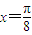 时,
时,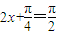 ,∴
,∴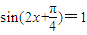 ,∴f(x)有最小值
,∴f(x)有最小值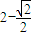 ,故②正确;
,故②正确; π,-
π,- π]时,
π]时,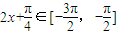 ,∴[-
,∴[- π,-
π,- π]是函数f(x)的一个单调递增区间,故③正确;
π]是函数f(x)的一个单调递增区间,故③正确;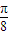 ,0)是函数g(x)=
,0)是函数g(x)=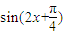 的一个对称中心,∴点(-
的一个对称中心,∴点(-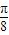 ,2)是函数f(x)的一个对称中心,故④正确
,2)是函数f(x)的一个对称中心,故④正确

 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案科目:高中数学 来源: 题型:阅读理解
查看答案和解析>>
科目:高中数学 来源: 题型:
| 全月应纳税所得额 | 税率(%) |
| 不超过1500元的部分 | 3 |
| 超过1500元至不超过4500元的部分 | 10 |
| 超过4500元至不超过9000元的部分 | 20 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| π | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:
已知函数f(x)与g(x)分别由下表给出:
|
查看答案和解析>>
科目:高中数学 来源: 题型:
| x |
1 | 2 | 3 | 4 | x |
1 | 2 | 3 | 4 |
| f(x) |
2 | 3 | 4 | 1 | g(x) |
2 | 1 | 4 | 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com