
【题目】【2017重庆二诊】已知函数![]() ,设关于
,设关于![]() 的方程
的方程![]() 有
有![]() 个不同的实数解,则
个不同的实数解,则![]() 的所有可能的值为( )
的所有可能的值为( )
A. 3 B. 1或3 C. 4或6 D. 3或4或6
科目:高中数学 来源: 题型:
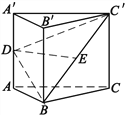
【题目】如图,正三棱柱![]() 中,
中,![]() 为
为![]() 中点,
中点,![]() 为
为![]() 上的一点,
上的一点,![]() .
.
(1)若![]() 平面
平面![]() ,求证:
,求证:![]() .
.
(2)平面![]() 将棱柱
将棱柱![]() 分割为两个几何体,记上面一个几何体的体积为
分割为两个几何体,记上面一个几何体的体积为![]() ,下面一个几何体的体积为
,下面一个几何体的体积为![]() ,求
,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市举办校园足球赛,组委会为了做好服务工作,招募了12名男志愿者和10名女志愿者,调查发现男女志愿者中分别有8人和4人喜欢看足球比赛,其余不喜欢
(1)根据以上数据完成以下2×2列联表:
喜欢看足球比赛 | 不喜欢看足球比赛 | 总计 | |
男 | |||
女 | |||
总计 |
(2)根据列联表的独立性检验,能否在犯错误的概率不超过0.10的前提下认为性别与喜欢看足球比赛有关?
(3)从女志愿者中抽取2人参加某场足球比赛服务工作,若其中喜欢看足球比赛的人数为ξ,求ξ的分布列和数学期望.
附:参考公式:K2= ![]() ,其中n=a+b+c+d
,其中n=a+b+c+d
参考数据:
P(K2≥k0) | 0.4 | 0.25 | 0.10 | 0.010 |
k0 | 0.708 | 1.323 | 2.706 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A、B、C所对的边长分别为a,b,c且满足csinA= ![]() acosC,则sinA+sinB的最大值是( )
acosC,则sinA+sinB的最大值是( )
A.1
B.![]()
C.3
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设集合A={(x,y)|(x﹣4)2+y2=1},B={(x,y)|(x﹣t)2+(y﹣at+2)2=1},如果命题“t∈R,A∩B≠”是真命题,则实数a的取值范围是( )
A.[1,4]
B.[0, ![]() ]
]
C.[0, ![]() ]
]
D.(﹣∞,0]∪( ![]() ,+∞]
,+∞]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 为椭圆
为椭圆![]() 上的一个动点,弦
上的一个动点,弦![]() 分别过左右焦点
分别过左右焦点![]() ,且当线段
,且当线段![]() 的中点在
的中点在![]() 轴上时,
轴上时, ![]() .
.
(1)求该椭圆的离心率;(2)设![]() ,试判断
,试判断![]() 是否为定值?若是定值,求出该定值,并给出证明;若不是定值,请说明理由.
是否为定值?若是定值,求出该定值,并给出证明;若不是定值,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分为16分)设A,B分别为椭圆![]()
![]() 的左、右顶点,椭圆的长轴长为
的左、右顶点,椭圆的长轴长为![]() ,且点
,且点![]() 在该椭圆上.
在该椭圆上.
(1)求椭圆的方程;
(2)设![]() 为直线
为直线![]() 上不同于点
上不同于点![]() 的任意一点,若直线
的任意一点,若直线![]() 与椭圆相交于异于
与椭圆相交于异于![]() 的点
的点![]() ,证明:△
,证明:△![]() 为钝角三角形.
为钝角三角形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com