
如图1,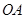 ,
,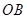 是某地一个湖泊的两条互相垂直的湖堤,线段
是某地一个湖泊的两条互相垂直的湖堤,线段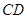 和曲线段
和曲线段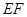 分别是湖泊中的一座栈桥和一条防波堤.为观光旅游的需要,拟过栈桥
分别是湖泊中的一座栈桥和一条防波堤.为观光旅游的需要,拟过栈桥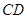 上某点
上某点 分别修建与
分别修建与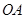 ,
,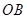 平行的栈桥
平行的栈桥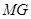 、
、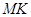 ,且以
,且以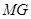 、
、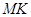 为边建一个跨越水面的三角形观光平台
为边建一个跨越水面的三角形观光平台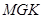 .建立如图2所示的直角坐标系,测得线段
.建立如图2所示的直角坐标系,测得线段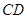 的方程是
的方程是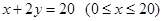 ,曲线段
,曲线段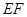 的方程是
的方程是 ,设点
,设点 的坐标为
的坐标为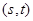 ,记
,记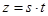 .(题中所涉及的长度单位均为米,栈桥和防波堤都不计宽度)
.(题中所涉及的长度单位均为米,栈桥和防波堤都不计宽度)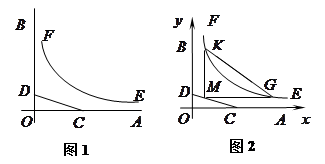
(1)求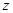 的取值范围;
的取值范围;
(2)试写出三角形观光平台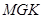 面积
面积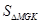 关于
关于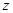 的函数解析式,并求出该面积的最小值
的函数解析式,并求出该面积的最小值
科目:高中数学 来源: 题型:解答题
作为绍兴市2013年5.1劳动节系列活动之一的花卉展在镜湖湿地公园举行.现有一占地1800平方米的矩形地块,中间三个矩形设计为花圃(如图),种植有不同品种的观赏花卉,周围则均是宽为1米的赏花小径,设花圃占地面积为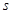 平方米,矩形一边的长为
平方米,矩形一边的长为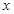 米(如图所示)
米(如图所示)
(1)试将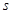 表示为
表示为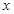 的函数;
的函数;
(2)问应该如何设计矩形地块的边长,使花圃占地面积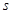 取得最大值.
取得最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知二次函数f(x)有两个零点0和-2,且f(x)最小值是-1,函数g(x)与f(x)的图像关于原点对称.
(1)求f(x)和g(x)的解析式;
(2)若h(x)=f(x)-λg(x)在区间[-1,1]上是增函数,求实数λ的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某连锁分店销售某种商品,每件商品的成本为4元,并且每件商品需向总店交 元(1≤a≤3)的管理费,预计当每件商品的售价为
元(1≤a≤3)的管理费,预计当每件商品的售价为 元(8≤x≤9)时,一年的销售量为(10-x)2万件.
元(8≤x≤9)时,一年的销售量为(10-x)2万件.
(1)求该连锁分店一年的利润L(万元)与每件商品的售价x的函数关系式L(x);
(2)当每件商品的售价为多少元时,该连锁分店一年的利润L最大,并求出L的最
大值M(a).
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
森林失火了,火正以 的速度顺风蔓延,消防站接到报警后立即派消防员前去,在失火后
的速度顺风蔓延,消防站接到报警后立即派消防员前去,在失火后 到达现场开始救火,已知消防队在现场每人每分钟平均可灭火
到达现场开始救火,已知消防队在现场每人每分钟平均可灭火 ,所消耗的灭火材料、劳务津贴等费用每人每分钟
,所消耗的灭火材料、劳务津贴等费用每人每分钟 元,另附加每次救火所损耗的车辆、器械和装备等费用平均每人
元,另附加每次救火所损耗的车辆、器械和装备等费用平均每人 元,而每烧毁
元,而每烧毁 森林的损失费为
森林的损失费为 元,设消防队派了
元,设消防队派了 名消防员前去救火,从到达现场开始救火到火全部扑灭共耗时
名消防员前去救火,从到达现场开始救火到火全部扑灭共耗时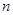
 .
.
(1)求出 与
与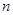 的关系式;
的关系式;
(2)问 为何值时,才能使总损失最小.
为何值时,才能使总损失最小.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
2013年某工厂生产某种产品,每日的成本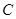 (单位:万元)与日产量
(单位:万元)与日产量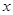 (单位:吨)满足函数关系式
(单位:吨)满足函数关系式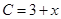 ,每日的销售额
,每日的销售额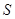 (单位:万元)与日产量
(单位:万元)与日产量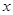 的函数关系式
的函数关系式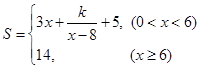
已知每日的利润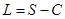 ,且当
,且当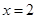 时,
时,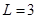 .
.
(1)求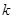 的值;
的值;
(2)当日产量为多少吨时,每日的利润可以达到最大,并求出最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com