
已知函数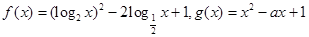
(1)求函数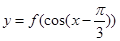 的定义域;
的定义域;
(2)若存在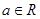 ,对任意
,对任意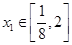 ,总存在唯一
,总存在唯一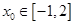 ,使得
,使得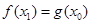 成立.求实数
成立.求实数 的取值范围.
的取值范围.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
已知函数f(x)=x2+2ax+3,x∈[-4,6].
(1)当a=-2时,求f(x)的最值;
(2)求实数a的取值范围,使y=f(x)在区间[-4,6]上是单调函数;
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某产品在一个生产周期内的总产量为100t,平均分成若干批生产。设每批生产需要投入固定费用75元,而每批生产直接消耗的费用与产品数量x的平方成正比,已知每批生产10t时,直接消耗的费用为300元(不包括固定的费用)。
(1)若每批产品数量为20t,求此产品在一个生产周期的总费用(固定费用和直接消耗的费用)。
(2)设每批产品数量为xt,一个生产周期内的总费用y元,求y与x的函数关系式,并求
出y的最小值。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某水域一艘装载浓硫酸的货船发生侧翻,导致浓硫酸泄漏,对河水造成了污染.为减
少对环境的影响,环保部门迅速反应,及时向污染河道投入固体碱,个单位的固体碱在水中
逐渐溶化,水中的碱浓度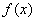 与时间
与时间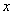 (小时)的关系可近似地表示为:
(小时)的关系可近似地表示为: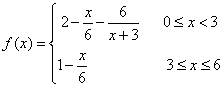 ,只有当污染河道水中碱的浓度不低于
,只有当污染河道水中碱的浓度不低于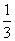 时,才能对污
时,才能对污
染产生有效的抑制作用.
(1)如果只投放1个单位的固体碱,则能够维持有效的抑制作用的时间有多长?
(2)第一次投放1单位固体碱后,当污染河道水中的碱浓度减少到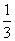 时,马上再投放1个单
时,马上再投放1个单
位的固体碱,设第二次投放后水中碱浓度为 ,求
,求 的函数式及水中碱浓度的最大值.
的函数式及水中碱浓度的最大值.
(此时水中碱浓度为两次投放的浓度的累加)
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图1,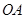 ,
,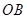 是某地一个湖泊的两条互相垂直的湖堤,线段
是某地一个湖泊的两条互相垂直的湖堤,线段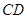 和曲线段
和曲线段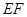 分别是湖泊中的一座栈桥和一条防波堤.为观光旅游的需要,拟过栈桥
分别是湖泊中的一座栈桥和一条防波堤.为观光旅游的需要,拟过栈桥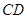 上某点
上某点 分别修建与
分别修建与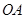 ,
,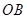 平行的栈桥
平行的栈桥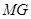 、
、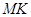 ,且以
,且以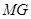 、
、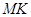 为边建一个跨越水面的三角形观光平台
为边建一个跨越水面的三角形观光平台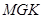 .建立如图2所示的直角坐标系,测得线段
.建立如图2所示的直角坐标系,测得线段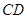 的方程是
的方程是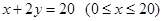 ,曲线段
,曲线段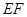 的方程是
的方程是 ,设点
,设点 的坐标为
的坐标为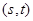 ,记
,记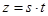 .(题中所涉及的长度单位均为米,栈桥和防波堤都不计宽度)
.(题中所涉及的长度单位均为米,栈桥和防波堤都不计宽度)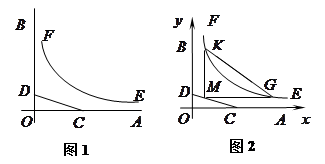
(1)求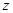 的取值范围;
的取值范围;
(2)试写出三角形观光平台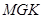 面积
面积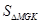 关于
关于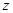 的函数解析式,并求出该面积的最小值
的函数解析式,并求出该面积的最小值
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某企业生产A,B两种产品,根据市场调查与预测,A产品的利润与投资成正比,其关系如图1;B产品的利润与投资的算术平方根成正比,其关系如图2(注:利润和投资单位:万元).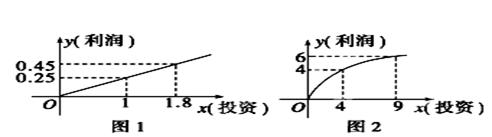
(1)分别将A、B两种产品的利润表示为投资的函数关系式;
(2)已知该企业已筹集到18万元资金,并将全部投入A,B两种产品的生产.
①若平均投入生产两种产品,可获得多少利润?
②问:如果你是厂长,怎样分配这18万元投资,才能使该企业获得最大利润?其最大利润约为多少万元?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图所示,在边长为60 cm的正方形铁片的四角上切去相等的正方形,再把它沿虚线折起,做成一个无盖的长方体箱子,箱底的边长是多少时,箱子的容积最大?最大容积是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com