
某产品在一个生产周期内的总产量为100t,平均分成若干批生产。设每批生产需要投入固定费用75元,而每批生产直接消耗的费用与产品数量x的平方成正比,已知每批生产10t时,直接消耗的费用为300元(不包括固定的费用)。
(1)若每批产品数量为20t,求此产品在一个生产周期的总费用(固定费用和直接消耗的费用)。
(2)设每批产品数量为xt,一个生产周期内的总费用y元,求y与x的函数关系式,并求
出y的最小值。
科目:高中数学 来源: 题型:解答题
已知二次函数f(x)满足条件f(0)=1和f(x+1)-f(x)=2x.
(1)求f(x);
(2)求f(x)在区间[-1,1]上的最大值和最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知幂函数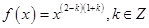 ,且
,且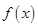 在
在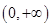 上单调递增.
上单调递增.
(1)求实数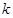 的值,并写出相应的函数
的值,并写出相应的函数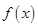 的解析式;
的解析式;
(2)若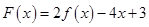 在区间
在区间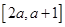 上不单调,求实数
上不单调,求实数 的取值范围;
的取值范围;
(3)试判断是否存在正数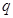 ,使函数
,使函数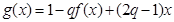 在区间
在区间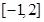 上的值域为
上的值域为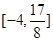 若存在,求出
若存在,求出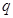 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
作为绍兴市2013年5.1劳动节系列活动之一的花卉展在镜湖湿地公园举行.现有一占地1800平方米的矩形地块,中间三个矩形设计为花圃(如图),种植有不同品种的观赏花卉,周围则均是宽为1米的赏花小径,设花圃占地面积为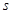 平方米,矩形一边的长为
平方米,矩形一边的长为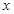 米(如图所示)
米(如图所示)
(1)试将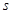 表示为
表示为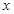 的函数;
的函数;
(2)问应该如何设计矩形地块的边长,使花圃占地面积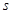 取得最大值.
取得最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某工厂生产一种仪器的元件,由于受生产能力和技术水平的限制,会产生一些次品,根据经验知道,其次品率P与日产量x(万件)之间大体满足关系: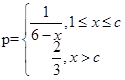 (其中c为小于6的正常数). (注:次品率=次品数/生产量,如P=0.1表示每生产10件产品,有1件为次品,其余为合格品),已知每生产1万件合格的元件可以盈利2万元,但每生产出1万件次品将亏损1万元,故厂方希望定出合适的日产量.
(其中c为小于6的正常数). (注:次品率=次品数/生产量,如P=0.1表示每生产10件产品,有1件为次品,其余为合格品),已知每生产1万件合格的元件可以盈利2万元,但每生产出1万件次品将亏损1万元,故厂方希望定出合适的日产量.
(1)试将生产这种仪器的元件每天的盈利额T(万元)表示为日产量x(万件)的函数;
(2)当日产量为多少时,可获得最大利润?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知二次函数f(x)有两个零点0和-2,且f(x)最小值是-1,函数g(x)与f(x)的图像关于原点对称.
(1)求f(x)和g(x)的解析式;
(2)若h(x)=f(x)-λg(x)在区间[-1,1]上是增函数,求实数λ的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
欲修建一横断面为等腰梯形(如图1)的水渠,为降低成本必须尽量减少水与渠壁的接触面,若水渠横断面面积设计为定值S,渠深h,则水渠壁的倾角α(0°<α<90°)应为多大时,方能使修建成本最低?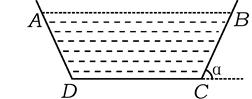
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com