
欲修建一横断面为等腰梯形(如图1)的水渠,为降低成本必须尽量减少水与渠壁的接触面,若水渠横断面面积设计为定值S,渠深h,则水渠壁的倾角α(0°<α<90°)应为多大时,方能使修建成本最低?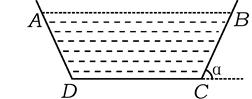
当α=60°时,修建成本最低.
解析试题分析:作BE⊥DC于E(图略),在Rt△BEC中,BC=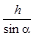 ,CE=hcotα,又AB-CD=2CE=2hcotα,AB+CD=
,CE=hcotα,又AB-CD=2CE=2hcotα,AB+CD=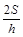 ,故CD=
,故CD=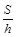 -hcotα.
-hcotα.
设y=AD+DC+BC,则y=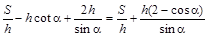 (0°<α<90°),由于S与h是常量,欲使y最小,只需u=
(0°<α<90°),由于S与h是常量,欲使y最小,只需u=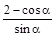 取最小值,u可看作(0,2)与(-sinα,cosα)两点连线的斜率,由于α∈(0°,90°),点(-sinα,cosα)在曲线x2+y2=1(-1<x<0,0<y<1)上运动,当过(0,2)的直线与曲线相切时,直线斜率最小,此时切点为(-
取最小值,u可看作(0,2)与(-sinα,cosα)两点连线的斜率,由于α∈(0°,90°),点(-sinα,cosα)在曲线x2+y2=1(-1<x<0,0<y<1)上运动,当过(0,2)的直线与曲线相切时,直线斜率最小,此时切点为(-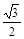 ,
,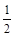 ),则有sinα=
),则有sinα=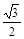 ,且cosα=
,且cosα=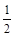 ,那么α=60°,故当α=60°时,修建成本最低.
,那么α=60°,故当α=60°时,修建成本最低.
考点:三角函数的运用
点评:解决的关键是根据三角函数的定义表示边长和长度,以及修建的成本,属于中档题。


科目:高中数学 来源: 题型:解答题
某产品在一个生产周期内的总产量为100t,平均分成若干批生产。设每批生产需要投入固定费用75元,而每批生产直接消耗的费用与产品数量x的平方成正比,已知每批生产10t时,直接消耗的费用为300元(不包括固定的费用)。
(1)若每批产品数量为20t,求此产品在一个生产周期的总费用(固定费用和直接消耗的费用)。
(2)设每批产品数量为xt,一个生产周期内的总费用y元,求y与x的函数关系式,并求
出y的最小值。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图所示,在边长为60 cm的正方形铁片的四角上切去相等的正方形,再把它沿虚线折起,做成一个无盖的长方体箱子,箱底的边长是多少时,箱子的容积最大?最大容积是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知二次函数 .
.
(1)若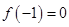 ,试判断函数
,试判断函数 零点个数;
零点个数;
(2)是否存在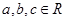 ,使
,使 同时满足以下条件
同时满足以下条件
①对任意 ,且
,且 ;
;
②对任意 ,都有
,都有 。若存在,求出
。若存在,求出 的值,若不存在,请说明理由。
的值,若不存在,请说明理由。
(3)若对任意 且
且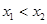 ,
, ,试证明存在
,试证明存在 ,
,
使 成立。
成立。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,一水渠的横断面是抛物线形,O是抛物线的顶点,口宽EF=4米,高3米建立适当的直角坐标系,求抛物线方程.
现将水渠横断面改造成等腰梯形ABCD,要求高度不变,只挖土,不填土,求梯形ABCD的下底AB多大时,所挖的土最少? 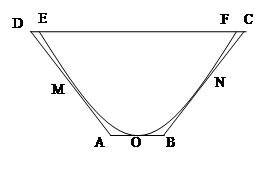
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题12分)某旅游景点预计2013年1月份起前
 个月的旅游人数的和
个月的旅游人数的和 (单位:万人)与
(单位:万人)与 的关系近似满足
的关系近似满足 已知第
已知第 月的人均消费额
月的人均消费额 (单位:元)与
(单位:元)与 的近似关系是
的近似关系是
(1)写出2013年第x月的旅游人数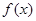 (单位:万人)与x的函数关系式;
(单位:万人)与x的函数关系式;
(2)试问2013年哪个月的旅游消费总额最大,最大旅游消费额为多少万元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com