
已知二次函数f(x)满足条件f(0)=1和f(x+1)-f(x)=2x.
(1)求f(x);
(2)求f(x)在区间[-1,1]上的最大值和最小值.
(1)f(x)=x2-x+1
(2)f(x)的最小值是f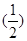 =
= ,f(x)的最大值是f(-1)=3.
,f(x)的最大值是f(-1)=3.
解析试题分析:(1)设f(x)=ax2+bx+c,由f(0)=1可知c=1.
而f(x+1)-f(x)=[a(x+1)2+b(x+1)+c]-(ax2+bx+c)=2ax+a+b.
由已知f(x+1)-f(x)=2x,可得2a=2,a+b=0.因而a=1,b=-1.
故f(x)=x2-x+1.
(2)∵f(x)=x2-x+1=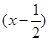 2+
2+ ,
,
又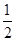 ∈[-1,1].
∈[-1,1].
∴当x∈[-1,1]时f(x)的最小值是f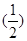 =
= ,
,
f(x)的最大值是f(-1)=3.
考点:函数的最值
点评:主要是考查了函数的最值的运用,属于基础题。


科目:高中数学 来源: 题型:解答题
“活水围网”养鱼技术具有养殖密度高、经济效益好的特点.研究表明:“活水围网”养鱼时,某种鱼在一定的条件下,每尾鱼的平均生长速度 (单位:千克/年)是养殖密度
(单位:千克/年)是养殖密度 (单位:尾/立方米)的函数.当
(单位:尾/立方米)的函数.当 不超过4(尾/立方米)时,
不超过4(尾/立方米)时, 的值为
的值为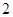 (千克/年);当
(千克/年);当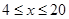 时,
时, 是
是 的一次函数;当
的一次函数;当 达到
达到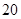 (尾/立方米)时,因缺氧等原因,
(尾/立方米)时,因缺氧等原因, 的值为
的值为 (千克/年).
(千克/年).
(1)当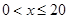 时,求函数
时,求函数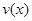 的表达式;
的表达式;
(2)当养殖密度 为多大时,鱼的年生长量(单位:千克/立方米)
为多大时,鱼的年生长量(单位:千克/立方米)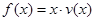 可以达到最大,并求出最大值.
可以达到最大,并求出最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数f(x)=ax2+2x+c(a、c∈N*)满足:①f(1)=5;②6<f(2)<11.
(1)求a、c的值;
(2)若对任意的实数x∈ ,都有f(x)-2mx≤1成立,求实数m的取值范围.
,都有f(x)-2mx≤1成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某工厂某种产品的年固定成本为250万元,每生产 千件,需另投入成本为
千件,需另投入成本为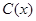 ,当年产量不足80千件时,
,当年产量不足80千件时,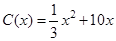 (万元).当年产量不小于80千件时,
(万元).当年产量不小于80千件时,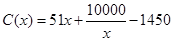 (万元),每件商品售价为0.05万元,通过市场分析,该厂生产的商品能全部售完.
(万元),每件商品售价为0.05万元,通过市场分析,该厂生产的商品能全部售完.
(Ⅰ)写出年利润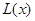 (万元)关于年产量
(万元)关于年产量 (千件)的函数解析式;
(千件)的函数解析式;
(Ⅱ)年产量为多少千件时,该厂在这一商品的生产中所获利润最大?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数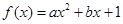 (
(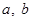 为实数,
为实数,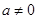 ,
,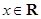 ),
),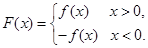
(Ⅰ)若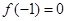 ,且函数
,且函数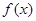 的值域为
的值域为 ,求
,求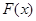 的表达式;
的表达式;
(Ⅱ)在(Ⅰ)的条件下,当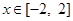 时,
时, 是单调函数,求实数
是单调函数,求实数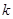 的取值范围;
的取值范围;
(Ⅲ)设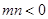 ,
,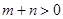 ,
,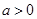 ,且函数
,且函数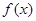 为偶函数,判断
为偶函数,判断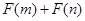 是否大于
是否大于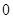 ?
?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数f(x)=x2+2ax+3,x∈[-4,6].
(1)当a=-2时,求f(x)的最值;
(2)求实数a的取值范围,使y=f(x)在区间[-4,6]上是单调函数;
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某产品在一个生产周期内的总产量为100t,平均分成若干批生产。设每批生产需要投入固定费用75元,而每批生产直接消耗的费用与产品数量x的平方成正比,已知每批生产10t时,直接消耗的费用为300元(不包括固定的费用)。
(1)若每批产品数量为20t,求此产品在一个生产周期的总费用(固定费用和直接消耗的费用)。
(2)设每批产品数量为xt,一个生产周期内的总费用y元,求y与x的函数关系式,并求
出y的最小值。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com