练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知.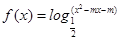
    ①若函数f(x)的值域为R，求实数m的取值范围；
    ②若函数f(x)在区间（－∞，1－）上是增函数，求实数m的取值范围.

    ① ;②.

    解析试题分析：①根据复合函数中的对数函数和二次函数的图像和性质解题确定m的取值；②由复合函数的性质，结合二次函数的图像解题，判断区间端点与对称轴的位置关系，注意复合函数单调性的判断是本题的关键.
    试题解析：①设,
    要使得函数的值域为R，则能取遍所有的正数,            2分
    则有,                                4分
    解得;                                 6分
    ②函数的底数是，那么若函数f(x)在区间（－∞，1－）上是增函数,
    函数在区间上是减函数,                   8分
    则有,                           10分
    解得.                                  12分
    考点：复合函数的性质，对数函数和二次函数的图像和性质的应用.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    已知函数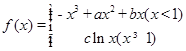的图像在点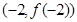处的切线方程为.
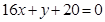    （Ⅰ）求实数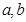的值；
    （Ⅱ）求函数在区间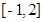上的最大值；
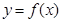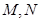    （Ⅲ）若曲线上存在两点使得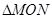是以坐标原点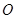为直角顶点的直角三角形，且斜边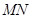的中点在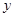轴上，求实数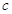的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    函数.若的定义域为，求实数的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    已知函数是二次函数，不等式的解集是，且在区间上的最大值为12．
    （1）求的解析式；
    （2）设函数在上的最小值为，求的表达式．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

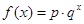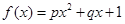    （本小题满分13分）某沿海地区养殖的一种特色海鲜上市时间仅能持续5个月，预测上市初期和后期会因供应不足使价格呈持续上涨态势，而中期又将出现供大于求，使价格连续下跌．现有三种价格模拟函数：①；②；③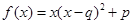．（以上三式中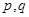均为常数，且）
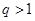    （1）为准确研究其价格走势，应选哪种价格模拟函数(不必说明理由)
    （2）若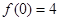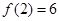，，求出所选函数的解析式（注：函数定义域是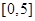．其中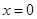表示8月1日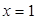，表示9月1日，…，以此类推）；
    （3）在（2）的条件下研究下面课题：为保证养殖户的经济效益，当地政府计划在价格下跌期间积极拓宽外销，请你预测该海鲜将在哪几个月份内价格下跌．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    已知二次函数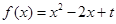与两坐标轴分别交于不同的三点A、B、C.
    （1）求实数t的取值范围；
    （2）当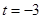时，求经过A、B、C三点的圆F的方程；
    （3）过原点作两条相互垂直的直线分别交圆F于M、N、P、Q四点，求四边形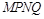的面积的最大值。

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    某工厂某种产品的年固定成本为250万元，每生产千件，需另投入成本为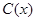，当年产量不足80千件时，（万元）.当年产量不小于80千件时，（万元）.每件商品售价为0.05万元.通过市场分析，该厂生产的商品能全部售完.
    （Ⅰ）写出年利润（万元）关于年产量（千件）的函数解析式；
    （Ⅱ）年产量为多少千件时，该厂在这一商品的生产中所获利润最大？

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    求出所有的函数使得对于所有，都能被整除.

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    已知二次函数f(x)满足条件f(0)＝1和f(x＋1)－f(x)＝2x.
    (1)求f(x)；
    (2)求f(x)在区间[－1,1]上的最大值和最小值．

    查看答案和解析>>

    同步练习册答案