已知函数
是二次函数，不等式
的解集是
，且在区间
上的最大值为12．
（1）求的解析式；
（2）设函数在
上的最小值为
，求的表达式．
科学实验活动册系列答案科目：高中数学 来源： 题型：解答题
设函数
，
，其中实数
．
（1）若
，求函数
的单调区间；
（2）当函数
与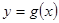
的图象只有一个公共点且
存在最小值时，记的最小值为
，求的值域；
（3）若与在区间
内均为增函数，求实数
的取值范围．
查看答案和解析>>
科目：高中数学 来源： 题型：解答题
某投资公司年初用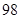
万元购置了一套生产设备并即刻生产产品，已知与生产产品相关的各种配套费用第一年需要支出
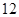万元，第二年需要支出
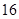万元，第三年需要支出
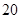万元，……，每年都比上一年增加支出
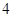万元，而每年的生产收入都为
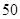万元．假设这套生产设备投入使用
年，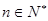
，生产成本等于生产设备购置费与这年生产产品相关的各种配套费用的和，生产总利润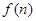
等于这年的生产收入与生产成本的差. 请你根据这些信息解决下列问题：
（Ⅰ）若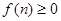
，求的值；
（Ⅱ）若干年后，该投资公司对这套生产设备有两个处理方案：
方案一：当年平均生产利润取得最大值时，以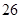
万元的价格出售该套设备；
方案二：当生产总利润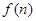取得最大值时，以
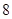万元的价格出售该套设备． 你认为哪个方案更合算？请说明理由．
查看答案和解析>>
科目：高中数学 来源： 题型：解答题
“活水围网”养鱼技术具有养殖密度高、经济效益好的特点．研究表明：“活水围网”养鱼时，某种鱼在一定的条件下，每尾鱼的平均生长速度
（单位：千克/年）是养殖密度
（单位：尾/立方米）的函数．当不超过4（尾/立方米）时，的值为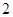
（千克/年）；当
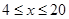时，是的一次函数；当达到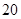
（尾/立方米）时，因缺氧等原因，的值为
（千克/年）．
（1）当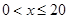
时，求函数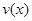
的表达式；
（2）当养殖密度为多大时，鱼的年生长量（单位：千克/立方米）
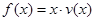可以达到最大，并求出最大值．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
；（2）①当
，即
时，
；
时，
；③当
，即
时，
．
，再讨论对称轴是在区间
上，还是在区间外，分别得
可设
2分
在区间
上的最大值是
由已知，得
5分
． 6分
，开口向上，对称轴为
； 10分
；
，不等式
恒成立，求
的取值范围.
的函数
满足
,当
∈
时，
时，求
恒成立，求实数
的取值范围．
且
，函数
，
，记
.
的定义域
的表达式及其零点；
的方程
在区间
内仅有一解，求实数
的取值范围.
（
）在区间
上有最大值
和最小值
．设
， 
、
的值；
在
上有解，求实数
的取值范围.
.
）上是增函数，求实数m的取值范围.