Question

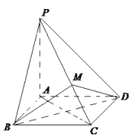
【题目】如图，在四棱锥中，四边形为正方形， 平面， ， 是上一点，且.

（1）求证： 平面；

（2）求直线与平面所成角的正弦值.

Answer 1

【答案】（1）证明见解析；（2）.

【解析】试题分析：

（1）连接，由线面垂直的性质定理可得，且，故平面， ，又，利用线面垂直的判断定理可得平面.

（2）法1：由（1）知平面，即是直线与平面所成角，设，则， ， ，结合几何关系计算可得，即直线与平面所成角的正弦值为.

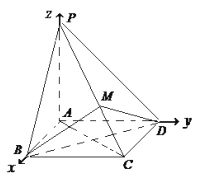
法2：取为原点，直线， ， 分别为， ， 轴，建立坐标系，不妨设，结合(1)的结论可得平面得法向量，而，据此计算可得直线与平面所成角的正弦值为.

试题解析：

（1）连接，由平面， 平面得，

又， ，

∴平面，得，

又， ，

∴平面.

（2）法1：由（1）知平面，即是直线与平面所成角，易证，而，

不妨设，则， ， ，

在中，由射影定理得，

可得，所以，

故直线与平面所成角的正弦值为.

法2：取为原点，直线， ， 分别为， ， 轴，建立坐标系，不妨设，则， ， ，

由（1）知平面得法向量，而，

∴ .

故直线与平面所成角的正弦值为.