
若函数 的定义域为
的定义域为 ,且满足
,且满足 为 奇函数,
为 奇函数, 为偶函数,则下列说法中一定正确的有
为偶函数,则下列说法中一定正确的有
(1) 的图像关于直线
的图像关于直线 对称
对称
(2) 的周期为
的周期为
(3)
(4) 在
在 上只有一个零点
上只有一个零点
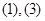
解析试题分析:因为,函数 的定义域为
的定义域为 ,且满足
,且满足 为 奇函数,
为 奇函数, 为偶函数,所以f(-x+1)=-f(x+1) .......(1);f(x-1)=f(-x-1).......(2)。
为偶函数,所以f(-x+1)=-f(x+1) .......(1);f(x-1)=f(-x-1).......(2)。
由(1) 得f(x+1)=-f(-x+1) ,故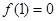 ;
;
由(2) 得f(x-1)=f(-x-1),故 的图像关于直线
的图像关于直线 对称;(1)正确。由此可知,函数
对称;(1)正确。由此可知,函数 在
在 要吗没零点,要吗不只一个零点;(4)不正确。
要吗没零点,要吗不只一个零点;(4)不正确。
由①令-x+1=t得:f(t)=-f(2-t)…………③;②令-x-1=t得:f(t)= f(-2-t)………④;
由③、④得f(2-t)=- f(-2-t)由此令-2-t=m得f(4+m) =-f(m),
所以,f(8+m) =-f(m+4)= f(m),函数f(x)的周期为8,(2)不正确。
所以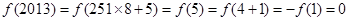 ,(3)正确。
,(3)正确。
综上知,答案为(1)(3)
考点:本题主要考查函数的奇偶性、周期性、对称性。
点评:中档题,本题比较典型,综合考查了函数的奇偶性、周期性、对称性,有一定难度,需要灵活运用“代换的方法”,寻求所需条件、结论。


湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com