
某农科所对冬季昼夜温差大小与某反季节大豆新品种发芽多少之间的关系进行分析研究,他们分别记录了12月1日至12月5日的每天昼夜温差与实验室每天每100棵种子中的发芽数,得到如下资料:
| 日期 | 12月 1日 | 12月 2日 | 12月 3日 | 12月 4日 | 12月 5日 |
| 温差x(℃) | 10 | 11 | 13 | 12 | 8 |
| 发芽数y(颗) | 23 | 25 | 30 | 26 | 16 |
该农科所确定的研究方案是:先从这5组数据中选取2组,用剩下的3组数据求线性回归方程,再对被选取的2组数据进行检验.
(1)求选取的2组数据恰好是不相邻2天数据的概率;
(2)若选取的是12月1日与12月5日的2组数据,请根据12月2日至12月4日的数据,求出y关于x的线性回归方程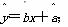
(3)若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过2颗,则认为得到的线性回归方程是可靠的,试问(2)中所得的线性回归方程是否可靠?
科目:高中数学 来源: 题型:
设椭圆C1:  +
+ =1(a>b>0),抛物线C2:x2+by=b2.
=1(a>b>0),抛物线C2:x2+by=b2.

(1)若C2经过C1的两个焦点,求C1的离心率;
(2)设A(0,b),Q(3 ,
, b),又M,N为C1与C2不在y轴上的两个交点,若△AMN的垂心为B(0,
b),又M,N为C1与C2不在y轴上的两个交点,若△AMN的垂心为B(0,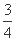 b),且△QMN的重心在C2上,求椭圆C1和抛物线C2的方程.
b),且△QMN的重心在C2上,求椭圆C1和抛物线C2的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
某单位200名职工的年龄分布情况如图,现要从中抽取40名职工作样本,用系统抽样法将全体职工随机按1~200编号,并按编号顺序平均分为40组(1~5号,6~10号,…,196~200号).若第5组抽出的号码为22,则第8组抽出的号码应是________.若用分层抽样方法,则40岁以下年龄段应抽取________人.
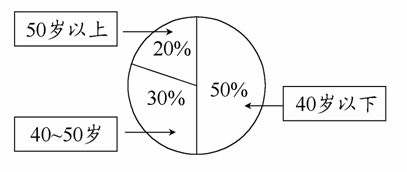
查看答案和解析>>
科目:高中数学 来源: 题型:
以下有关线性回归分析的说法不正确的是( )
A.通过最小二乘法得到的线性回归直线过样本点的中心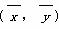
B.用最小二乘法求回归直线方程,是寻求使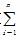 (yi-bxi-a)2最小的a,b的值
(yi-bxi-a)2最小的a,b的值
C.相关系数r越小,表示两个变量相关性越弱
D.R2=1-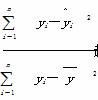 越接近1,表示回归的效果越好
越接近1,表示回归的效果越好
查看答案和解析>>
科目:高中数学 来源: 题型:
在一个袋子中装有分别标注数字1,2,3,4,5的五个小球,这些小球除标注的数字外完全相同.现从中随机取出2个小球,则取出的小球标注的数字之和为3或6的概率是( )
A. B.
B.
C. D.
D.
查看答案和解析>>
科目:高中数学 来源: 题型:
某公务员去开会,他乘火车、轮船、汽车、飞机去的概率分别为0.3、0.2、0.1、0.4.
(1)求他乘火车或乘飞机去开会的概率;
(2)求他不乘轮船去开会的概率;
(3)如果他乘某种交通工具去开会的概率为0.5,请问他有可能是乘何种交通工具去开会的?
查看答案和解析>>
科目:高中数学 来源: 题型:
某市为了了解今年高中毕业生的体能状况,从本市某校高中毕业班中抽取一个班进行铅球测试,成绩在8.0米(精确到0.1米)以上的为合格.把所得数据进行整理后,分成6组画出频率分布直方图的一部分(如图),已知从左到右前5个小组的频率分别为0.04,0.10,0.14,0.28,0.30.第6小组的频数是7.
(1)求这次铅球测试成绩合格的人数;
(2)若由直方图来估计这组数据的中位数,指出它在第几组内,并说明理由;
(3)若参加此次测试的学生中,有9人的成绩为优秀,现在要从成绩优秀的学生中,随机选出2人参加“毕业运动会”,已知a、b的成绩均为优秀,求两人至少有1人入选的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com