
【题目】《情境》刘晓红同学在做达标训练的课外作业时,遇到一个如何用五点法作出正弦型函数在长度为一个周期的闭区间上的图象及图象之间如何进行变换的问题,她犯愁了.
《问题》设函数![]() 的周期为
的周期为![]() ,且图象过点
,且图象过点![]() .
.
(1)求![]() 与
与![]() 的值;
的值;
(2)用五点法作函数![]() 在长度为一个周期的闭区间上的图象;
在长度为一个周期的闭区间上的图象;
(3)叙述函数![]() 的图象可由函数
的图象可由函数![]() 的图象经过怎样的变换而得到.
的图象经过怎样的变换而得到.
由于刘晓红对上述问题还没有掌握解决方法及解题概念和步骤,导致无从下手,于是她请教了班上的学习委员张倩同学给她做了如下点拨:
用五点法作出在一个周期的闭区间上的图象,首先要列表并分别令相位![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() ,再解出对应的
,再解出对应的![]() 、
、![]() 的值,得出坐标
的值,得出坐标![]() ,然后描点,最后画出图象.而由函数
,然后描点,最后画出图象.而由函数![]() 的图象变到函数
的图象变到函数![]() 的图象主要有两种途径:①按物理量初相
的图象主要有两种途径:①按物理量初相![]() ,周期
,周期![]() ,振幅
,振幅![]() 的顺序变换;②按物理量周期
的顺序变换;②按物理量周期![]() ,初相
,初相![]() ,振幅
,振幅![]() 的顺序变换.要注意两者操作的区别,防止出错.
的顺序变换.要注意两者操作的区别,防止出错.
经过张倩耐心而细致的解释,刘晓红豁然开朗,并对该题解答如下:
(注意:解答第(3)问时,要按照题中要求,写出两种变换过程)
【答案】(1)![]() ,
,![]() ;(2)见解析;(3)见解析.
;(2)见解析;(3)见解析.
【解析】
(1)由函数![]() 的最小正周期计算出
的最小正周期计算出![]() 的值,由该函数的图象过点
的值,由该函数的图象过点![]() ,结合
,结合![]() 的取值范围可求得
的取值范围可求得![]() 的值;
的值;
(2)分别令相位![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() ,再解出对应的
,再解出对应的![]() 、
、![]() 的值,得出坐标
的值,得出坐标![]() ,然后列表、描点、连线,可得出函数
,然后列表、描点、连线,可得出函数![]() 在长度为一个周期的闭区间上的图象;
在长度为一个周期的闭区间上的图象;
(3)利用三角函数图象变换规律可得出题中①②中由函数![]() 变换到函数
变换到函数![]() 的变换方法.
的变换方法.
(1)由函数![]() 的周期为
的周期为![]() ,且
,且![]() ,知
,知![]() ,解得
,解得![]() .
.
将点![]() 代入
代入![]() 中,有
中,有![]() ,且
,且![]() ,解得
,解得![]() ,
,
故![]() ,
,![]() ;
;
(2)由(1)知![]() ,
,
作出函数![]() 在一个周期
在一个周期![]() 上的图象.
上的图象.
①列表如下:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
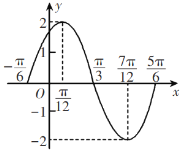
②先描点,再作出函数![]() 在一个周期
在一个周期![]() 上的图象,如图所示:
上的图象,如图所示:
③(方法一)先把![]() 的图象向左平移
的图象向左平移![]() 个单位长度,得到
个单位长度,得到![]() 的图象.
的图象.
再把![]() 的图象上所有点的纵坐标不变,横坐标缩短到原来的
的图象上所有点的纵坐标不变,横坐标缩短到原来的![]() ,得到
,得到![]() 的图象.
的图象.
最后把![]() 的图象上所有点的横坐标不变,纵坐标伸长到原来的
的图象上所有点的横坐标不变,纵坐标伸长到原来的![]() 倍,得到
倍,得到![]() 的图象;
的图象;
(方法二)先将![]() 的图象上所有点的纵坐标不变,横坐标变为原来的
的图象上所有点的纵坐标不变,横坐标变为原来的![]() ,得到
,得到![]() 的图象,
的图象,
把![]() 的图象向左平移
的图象向左平移![]() 个单位长度,得到
个单位长度,得到![]() 的图象.
的图象.
最后把![]() 的图象上所有点的横坐标不变,纵坐标伸长到原来的
的图象上所有点的横坐标不变,纵坐标伸长到原来的![]() 倍,得到
倍,得到![]() 的图象.
的图象.


科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以原点
为参数),以原点![]() 为极点,
为极点,![]() 轴正半轴为极轴,建立极坐标系,曲线
轴正半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的普通方程与曲线
的普通方程与曲线![]() 直角坐标方程;
直角坐标方程;
(2)设![]() 为曲线
为曲线![]() 上的动点,求点
上的动点,求点![]() 到
到![]() 上点的距离的最小值,并求此时点
上点的距离的最小值,并求此时点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校举行了一次考试,从学生中随机选取了![]() 人的成绩作为样本进行统计.已知这些学生的成绩全部在
人的成绩作为样本进行统计.已知这些学生的成绩全部在![]() 分至
分至![]() 分之间,现将成绩按如下方式分成
分之间,现将成绩按如下方式分成![]() 组:第一组
组:第一组![]() ,第二组
,第二组![]() ,.......,第六组
,.......,第六组![]() ,并据此绘制了如图所示的频率分布直方图.
,并据此绘制了如图所示的频率分布直方图.
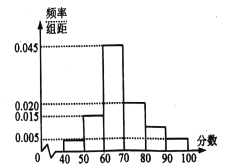
(1)估计这次月考数学成绩的平均分和众数;
(2)从成绩大于等于![]() 分的学生中随机抽取
分的学生中随机抽取![]() 人,求至少有
人,求至少有![]() 名学生的成绩在
名学生的成绩在![]() 内的概率.
内的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】比较甲、乙两名学生的数学学科素养的各项能力指标值(满分为5分,分值高者为优),绘制了如图所示的六维能力雷达图,例如图中甲的数学抽象指标值为4,乙的数学抽象指标值为5,则下面叙述正确的是( )
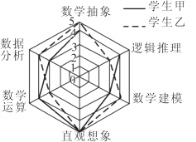
A.甲的逻辑推理能力指标值优于乙的逻辑推理能力指标值
B.甲的数学建模能力指标值优于乙的直观想象能力指标值
C.甲的六维能力指标值整体水平优于乙的六维能力指标值整体水平
D.甲的数学运算能力指标值优于甲的直观想象能力指标值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() 的离心率为
的离心率为![]() ,且经过点M(1,
,且经过点M(1,![]() ).
).
(1)求椭圆C的标准方程;
(2)已知直线l不过点P(0,1),与椭圆C交于A、B两点,记直线PA、PB的斜率分别为k1、k2,且满足k1+k2=1,求证:直线l过定点,并求出该定点坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“中国剩余定理”又称“孙子定理”.1852年英国来华传教士伟烈亚力将《孙子算经》中“物不知数”问题的解法传至欧洲.1874年英国数学家马西森指出此法符合1801年由高斯得到的关于同余式解法的一般性定理,因而西方称之为“中国剩余定理”,“中国剩余定理”讲的是一个关于整除的问题,现有这样一个整除问题:将1到2030这2030个自然数中,能被3除余1且被4除余1的数按从小到大的顺序排成一列,构成数列![]() ,则此数列共有( )
,则此数列共有( )
A.168项B.169项C.170项D.171项
查看答案和解析>>
科目:高中数学 来源: 题型:
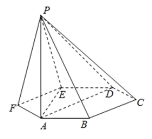
【题目】已知六棱锥![]() 的底面是正六边形,
的底面是正六边形,![]() 平面ABC,
平面ABC,![]() .则下列命题中正确的有( )
.则下列命题中正确的有( )
①平面![]() 平面PAE;
平面PAE;
②![]() ;
;
③直线CD与PF所成角的余弦值为![]() ;
;
④直线PD与平面ABC所成的角为45°;
⑤![]() 平面PAE.
平面PAE.
A.①④B.①③④C.②③⑤D.①②④⑤
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com