
【题目】如图①,在正方形![]() 的各边上分别取
的各边上分别取![]() 四点,使
四点,使![]() ,将正方形沿对角线
,将正方形沿对角线![]() 折起,如图②
折起,如图②
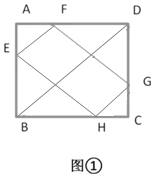
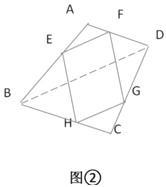
(1)证明:图②中![]() 为矩形;
为矩形;
(2)当二面角![]() 为多大时,
为多大时,![]() 为正方形.
为正方形.
【答案】(1)证明见解析;(2)当二面角A-BD-C为![]() 时,四边形EFGH为正方形
时,四边形EFGH为正方形
【解析】
(1)根据对应边成比例可得EF∥BD,HG∥BD,从而可得EF∥HG,即四边形EFGH为平行四边形,设O为BD的中点,连接AO,CO,BD,利用线面垂直的判定定理可得BD⊥平面AOC,从而可得BD⊥AC,进而可得EF⊥EH,即证.
(2)设AB=a,可得![]() ,由题意只需使EH=HG,根据比例可得
,由题意只需使EH=HG,根据比例可得![]() ,由∠AOC为二面角A-BD-C的平面角,AO=CO=AC,即可求得二面角A-BD-C为600.
,由∠AOC为二面角A-BD-C的平面角,AO=CO=AC,即可求得二面角A-BD-C为600.
(1)因为AE:EB=AF:FD,所以EF∥BD,
同理可得,HG∥BD,所以EF∥HG;
同理可得EH∥FG,所以四边形EFGH为平行四边形,
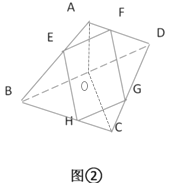
设O为BD的中点,连接AO,CO,BD,
BD⊥AO,BD⊥CO,所以BD⊥平面AOC,故BD⊥AC,
又因为BD∥EF,AC∥EH,所以EF⊥EH
所以EFGH为矩形
(2)设AB=a
则![]() ,
,
要使四边形EFGH为正方形,只需使EH=HG
![]() ,
,
由(1)可知∠AOC为二面角A-BD-C的平面角,且AO=CO=AC,
所以,当二面角A-BD-C为600时,四边形EFGH为正方形


科目:高中数学 来源: 题型:
【题目】设有一组圆![]() .下列四个命题正确的是( )
.下列四个命题正确的是( )
A. 存在![]() ,使圆与
,使圆与![]() 轴相切
轴相切
B. 存在一条直线与所有的圆均相交
C. 存在一条直线与所有的圆均不相交
D. 所有的圆均不经过原点
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),曲线
为参数),曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以该直角坐标系的原点
为参数),以该直角坐标系的原点![]() 为极点,
为极点,![]() 轴的非负半轴为极轴建立极坐标系,曲线
轴的非负半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(Ⅰ)分别求曲线![]() 的极坐标方程和曲线
的极坐标方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)设直线![]() 交曲线
交曲线![]() 于
于![]() ,
,![]() 两点,交曲线
两点,交曲线![]() 于
于![]() ,
,![]() 两点,求
两点,求![]() 的长.
的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2020年1月22日,国新办发布消息:新型冠状病毒来源于武汉一家海鲜市场非法销售的野生动.专家通过全基因组比对发现此病毒与2003年的非典冠状病毒以及此后的中东呼吸综合征冠状病毒,分别达到70%和40%的序列相似性.这种新型冠状病毒对人们的健康生命带来了严重威胁因此,某生物疫苗研究所加紧对新型冠状病毒疫苗进行实验,并将某一型号疫苗用在动物小白鼠身上进行科研和临床实验,得到统计数据如下:
未感染病毒 | 感染病毒 | 总计 | |
未注射疫苗 | 20 |
|
|
注射疫苗 | 30 |
|
|
总计 | 50 | 50 | 100 |
现从所有试验小白鼠中任取一只,取到“注射疫苗”小白鼠的概率为![]() .
.
(1)求![]() 列联表中的数据
列联表中的数据![]() ,
,![]() ,
,![]() ,
,![]() 的值;
的值;
(2)能否有99.9%把握认为注射此种疫苗对预防新型冠状病毒有效?
附:![]() .
.
| 0.05 | 0.01 | 0.005 | 0.001 |
| 3.841 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程:在平面直角坐标系![]() 中,曲线
中,曲线![]() :
:![]() (
(![]() 为参数),在以平面直角坐标系的原点为极点、
为参数),在以平面直角坐标系的原点为极点、![]() 轴的正半轴为极轴,且与平面直角坐标系
轴的正半轴为极轴,且与平面直角坐标系![]() 取相同单位长度的极坐标系中,曲线
取相同单位长度的极坐标系中,曲线![]() :
:![]() .
.
(1)求曲线![]() 的普通方程以及曲线
的普通方程以及曲线![]() 的平面直角坐标方程;
的平面直角坐标方程;
(2)若曲线![]() 上恰好存在三个不同的点到曲线
上恰好存在三个不同的点到曲线![]() 的距离相等,求这三个点的极坐标.
的距离相等,求这三个点的极坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,矩形![]() 垂直于直角梯形
垂直于直角梯形![]() ,
,![]() ,
,![]() 为
为![]() 中点,
中点,![]() ,
,![]() .
.
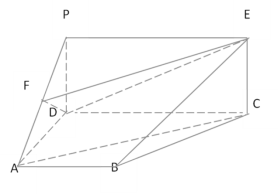
(1)求证:![]() ∥平面
∥平面![]() ;
;
(2)线段![]() 上是否存在点
上是否存在点![]() ,使
,使![]() 与平面
与平面![]() 所成角的正切值为
所成角的正切值为![]() ?若存在,请求出
?若存在,请求出![]() 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】袋子中放有大小和形状相同的小球若干,其中标号为0的小球1个,标号为1的小球1个,标号为2的小球n个,已知从袋子中随机抽取1个小球,取到标号为2的小球的概率是![]() .
.
(1)求n的值;
(2)从袋子中不放回地随机抽取2个球,记第一次取出小球标号为a,第二次取出的小球标号为b.①记“a+b=2”为事件A,求事件A的概率;
②在区间[0,2]内任取2个实数x,y,求事件“x2+y2>(a-b)2恒成立”的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《情境》刘晓红同学在做达标训练的课外作业时,遇到一个如何用五点法作出正弦型函数在长度为一个周期的闭区间上的图象及图象之间如何进行变换的问题,她犯愁了.
《问题》设函数![]() 的周期为
的周期为![]() ,且图象过点
,且图象过点![]() .
.
(1)求![]() 与
与![]() 的值;
的值;
(2)用五点法作函数![]() 在长度为一个周期的闭区间上的图象;
在长度为一个周期的闭区间上的图象;
(3)叙述函数![]() 的图象可由函数
的图象可由函数![]() 的图象经过怎样的变换而得到.
的图象经过怎样的变换而得到.
由于刘晓红对上述问题还没有掌握解决方法及解题概念和步骤,导致无从下手,于是她请教了班上的学习委员张倩同学给她做了如下点拨:
用五点法作出在一个周期的闭区间上的图象,首先要列表并分别令相位![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() ,再解出对应的
,再解出对应的![]() 、
、![]() 的值,得出坐标
的值,得出坐标![]() ,然后描点,最后画出图象.而由函数
,然后描点,最后画出图象.而由函数![]() 的图象变到函数
的图象变到函数![]() 的图象主要有两种途径:①按物理量初相
的图象主要有两种途径:①按物理量初相![]() ,周期
,周期![]() ,振幅
,振幅![]() 的顺序变换;②按物理量周期
的顺序变换;②按物理量周期![]() ,初相
,初相![]() ,振幅
,振幅![]() 的顺序变换.要注意两者操作的区别,防止出错.
的顺序变换.要注意两者操作的区别,防止出错.
经过张倩耐心而细致的解释,刘晓红豁然开朗,并对该题解答如下:
(注意:解答第(3)问时,要按照题中要求,写出两种变换过程)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com