
【题目】设函数![]() (
(![]() 且
且![]() )是定义域为
)是定义域为![]() 的奇函数.
的奇函数.
(1)若![]() ,试求不等式
,试求不等式![]() 的解集;
的解集;
(2)若![]() ,且
,且![]() ,求
,求![]() 在
在![]() 上的最小值.
上的最小值.
【答案】(Ⅰ)![]()
(Ⅱ)-2
【解析】
首先利用奇函数![]() 求得
求得![]() 的值.(1)根据
的值.(1)根据![]() 求得
求得![]() ,由此求得函数
,由此求得函数![]() 是单调递增函数,再根据函数的奇偶性和单调性求得不等式的解集.(2)利用
是单调递增函数,再根据函数的奇偶性和单调性求得不等式的解集.(2)利用![]() 求得
求得![]() 的值.由此求得函数
的值.由此求得函数![]() 的解析式.在利用换元法以及配方法求得函数
的解析式.在利用换元法以及配方法求得函数![]() 在给定区间上的最小值.
在给定区间上的最小值.
∵f(x)是定义域为R的奇函数,∴f(0)=0,∴k-1=0,∴k=1.
(1)∵f(1)>0,∴a-![]() >0,又a>0且a≠1,∴a>1.∵k=1,∴f(x)=ax-a-x,当a>1时,y=ax和y=-a-x在R上均为增函数,∴f(x)在R上为增函数,原不等式可化为f(x2+2x)>f(4-x),∴x2+2x>4-x,即x2+3x-4>0,∴x>1或x<-4,∴不等式的解集为{x|x>1或x<-4}.
>0,又a>0且a≠1,∴a>1.∵k=1,∴f(x)=ax-a-x,当a>1时,y=ax和y=-a-x在R上均为增函数,∴f(x)在R上为增函数,原不等式可化为f(x2+2x)>f(4-x),∴x2+2x>4-x,即x2+3x-4>0,∴x>1或x<-4,∴不等式的解集为{x|x>1或x<-4}.
(2)∵f(1)=![]() ,∴a-
,∴a-![]() =
=![]() ,即2a2-3a-2=0.∴a=2或a=-
,即2a2-3a-2=0.∴a=2或a=-![]() (舍去),∴g(x)=22x+2-2x-4(2x-2-x)=(2x-2-x)2-4(2x-2-x)+2,令t=h(x)=2x-2-x(x≥1),则g(t)=t2-4t+2.∵t=h(x)在[1,+∞)上为增函数(由(1)可知),∴h(x)≥h(1)=
(舍去),∴g(x)=22x+2-2x-4(2x-2-x)=(2x-2-x)2-4(2x-2-x)+2,令t=h(x)=2x-2-x(x≥1),则g(t)=t2-4t+2.∵t=h(x)在[1,+∞)上为增函数(由(1)可知),∴h(x)≥h(1)=![]() ,即t≥
,即t≥![]() ,g(t)=t2-4t+2=(t-2)2-2,t∈
,g(t)=t2-4t+2=(t-2)2-2,t∈![]() .∴当t=2时,g(t)取得最小值-2,即g(x)取得最小值-2,此时x=log2(1+
.∴当t=2时,g(t)取得最小值-2,即g(x)取得最小值-2,此时x=log2(1+![]() ),故当x=log2(1+
),故当x=log2(1+![]() )时,g(x)有最小值-2.
)时,g(x)有最小值-2.


 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案科目:高中数学 来源: 题型:
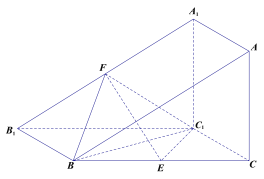
【题目】如图,三棱柱![]() 的侧面
的侧面![]() 是平行四边形,
是平行四边形,![]() ,平面
,平面![]() 平面
平面![]() ,且
,且![]() 分别是
分别是![]() 的中点.
的中点.
(1)求证:![]() 平面
平面![]() ;
;
(2)当侧面![]() 是正方形,且
是正方形,且![]() 时,
时,
(ⅰ)求二面角![]() 的大小;
的大小;
(ⅱ)在线段![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() ?若存在,指出点
?若存在,指出点![]() 的位置;若不存在,请说明理由.
的位置;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为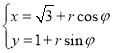 (
(![]() ,
,![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,
为极点,![]() 轴正半轴为极轴建立极坐标系,直线
轴正半轴为极轴建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() ,若直线
,若直线![]() 与曲线
与曲线![]() 相切;
相切;
(1)求曲线![]() 的极坐标方程与直线
的极坐标方程与直线![]() 的直角坐标方程;
的直角坐标方程;
(2)在曲线![]() 上取两点
上取两点![]() ,
,![]() 与原点
与原点![]() 构成
构成![]() ,且满足
,且满足![]() ,求
,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数![]() (其中
(其中![]() )的部分图象如图所示,把函数
)的部分图象如图所示,把函数![]() 的图像向右平移
的图像向右平移![]() 个单位长度,再向下平移1个单位,得到函数
个单位长度,再向下平移1个单位,得到函数![]() 的图像.
的图像.

(1)当![]() 时,求
时,求![]() 的值域
的值域
(2)令![]() ,若对任意
,若对任意![]() 都有
都有![]() 恒成立,求
恒成立,求![]() 的最大值
的最大值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,A,B,C三地有直道相通,其中AB、BC为步行道,AC为机动车道,已知A在B的正北方向6千米处,C在B的正东方向![]() 千米处,某校开展步行活动,从A地出发,经B地到达C地,中途不休息.
千米处,某校开展步行活动,从A地出发,经B地到达C地,中途不休息.

(1)媒体转播车从A出发,沿AC行至点P处,此时![]() ,求PB的距离;
,求PB的距离;
(2)媒体记者随队步行,媒体转播车从A地沿AC前往C,两者同时出发,步行的速度为6千米/小时,为配合转播,转播车的速度为12千米/小时,记者和转播车通过专用对讲机保持联系,转播车开到C地后原地等待,直到记者到达C地,若对讲机的有效通话距离不超过9千米,求他们通过对讲机能保持联系的总时长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司为了激励业务员的积极性,对业绩在60万到200万的业务员进行奖励奖励方案遵循以下原则:奖金y(单位:万元)随着业绩值x(单位:万元)的增加而增加,且奖金不低于1.5万元同时奖金不超过业绩值的5%.
(1)若某业务员的业绩为100万核定可得4万元奖金,若该公司用函数![]() (k为常数)作为奖励函数模型,则业绩200万元的业务员可以得到多少奖励?(已知
(k为常数)作为奖励函数模型,则业绩200万元的业务员可以得到多少奖励?(已知![]() ,
,![]() )
)
(2)若采用函数![]() 作为奖励函数模型试确定最小的正整数a的值.
作为奖励函数模型试确定最小的正整数a的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com