
【题目】如图,三棱柱![]() 的侧面
的侧面![]() 是平行四边形,
是平行四边形,![]() ,平面
,平面![]() 平面
平面![]() ,且
,且![]() 分别是
分别是![]() 的中点.
的中点.
(1)求证:![]() 平面
平面![]() ;
;
(2)当侧面![]() 是正方形,且
是正方形,且![]() 时,
时,
(ⅰ)求二面角![]() 的大小;
的大小;
(ⅱ)在线段![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() ?若存在,指出点
?若存在,指出点![]() 的位置;若不存在,请说明理由.
的位置;若不存在,请说明理由.
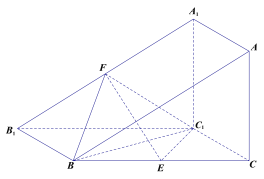
【答案】(1)见解析(2)(ⅰ)![]() (ⅱ)点
(ⅱ)点![]() 在点
在点![]() 处时,有
处时,有![]()
【解析】
(1)取![]() 中点
中点![]() ,证明四边形
,证明四边形![]() 是平行四边形,可得
是平行四边形,可得![]() 从而得证;
从而得证;
(2)(ⅰ)先证明![]() 平面
平面![]() 以
以![]() 为原点建立空间直角坐标系
为原点建立空间直角坐标系![]() ,求出平面
,求出平面![]() 与平面
与平面![]() 的法向量,即可得到二面角
的法向量,即可得到二面角![]() 的大小;
的大小;
(ⅱ)假设在线段![]() 上存在点
上存在点![]() ,使得
,使得![]() . 设
. 设![]() ,则
,则![]() .
.
利用垂直关系,建立![]() 的方程,解之即可.
的方程,解之即可.
证明:(1)取![]() 中点
中点![]() ,连
,连![]() ,连
,连![]() .
.

在△![]() 中,因为
中,因为![]() 分别是
分别是![]() 中点,
中点,
所以![]() ,且
,且![]() .
.
在平行四边形![]() 中,因为
中,因为![]() 是
是![]() 的中点,
的中点,
所以![]() ,且
,且![]() .
.
所以![]() ,且
,且![]() .
.
所以四边形![]() 是平行四边形.
是平行四边形.
所以![]() .
.
又因为![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.
(2)因为侧面![]() 是正方形,所以
是正方形,所以![]() .
.
又因为平面![]() 平面
平面![]() ,且平面
,且平面![]() 平面
平面![]()
所以![]() 平面
平面![]() .所以
.所以![]() .
.
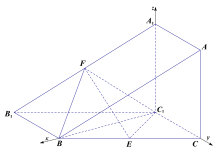
又因为![]() ,以
,以![]() 为原点建立空间直角坐标系
为原点建立空间直角坐标系![]() ,如图所示.
,如图所示.
设![]() ,则
,则![]() ,
,
![]() .
.
(ⅰ)设平面![]() 的一个法向量为
的一个法向量为![]() .
.
由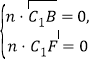 得
得 即
即![]() 令
令![]() ,所以
,所以![]() .
.
又因为![]() 平面
平面![]() ,所以
,所以![]() 是平面
是平面![]() 的一个法向量.
的一个法向量.
所以 .
.
由图可知,二面角![]() 为钝角,所以二面角
为钝角,所以二面角![]() 的大小为
的大小为![]() .
.
(ⅱ)假设在线段![]() 上存在点
上存在点![]() ,使得
,使得![]() .
.
设![]() ,则
,则![]() .
.
因为
![]()
![]() ,
,
又![]() ,
,
所以![]() .
.
所以![]() .
.
故点![]() 在点
在点![]() 处时,有
处时,有![]()


科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的两个焦点
的两个焦点![]() ,
,![]() ,且椭圆过点
,且椭圆过点![]() ,
,![]() ,且
,且![]() 是椭圆上位于第一象限的点,且
是椭圆上位于第一象限的点,且![]() 的面积
的面积![]() .
.
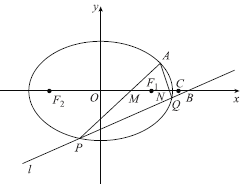
(1)求点![]() 的坐标;
的坐标;
(2)过点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 相交于点
相交于点![]() ,
,![]() ,直线
,直线![]() ,
,![]() 与
与![]() 轴相交于
轴相交于![]() ,
,![]() 两点,点
两点,点![]() ,则
,则![]() 是否为定值,如果是定值,求出这个定值,如果不是请说明理由.
是否为定值,如果是定值,求出这个定值,如果不是请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() ,点
,点![]() 在椭圆
在椭圆![]() 上,椭圆
上,椭圆![]() 的离心率是
的离心率是![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)设点![]() 为椭圆长轴的左端点,
为椭圆长轴的左端点,![]() 为椭圆上异于椭圆
为椭圆上异于椭圆![]() 长轴端点的两点,记直线
长轴端点的两点,记直线![]() 斜率分别为
斜率分别为![]() ,若
,若![]() ,请判断直线
,请判断直线![]() 是否过定点?若过定点,求该定点坐标,若不过定点,请说明理由.
是否过定点?若过定点,求该定点坐标,若不过定点,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某日A,B,C三个城市18个销售点的小麦价格如下表:
销售点序号 | 所属城市 | 小麦价格(元/吨) | 销售点序号 | 所属城市 | 小麦价格(元/吨) |
1 | A | 2420 | 10 | B | 2500 |
2 | C | 2580 | 11 | A | 2460 |
3 | C | 2470 | 12 | A | 2460 |
4 | C | 2540 | 13 | A | 2500 |
5 | A | 2430 | 14 | B | 2500 |
6 | C | 2400 | 15 | B | 2450 |
7 | A | 2440 | 16 | B | 2460 |
8 | B | 2500 | 17 | A | 2460 |
9 | A | 2440 | 18 | A | 2540 |
(1)甲以B市5个销售点小麦价格的中位数作为购买价格,乙从C市4个销售点中随机挑选2个了解小麦价格.记乙挑选的2个销售点中小麦价格比甲的购买价格高的个数为![]() ,求
,求![]() 的分布列及数学期望;
的分布列及数学期望;
(2)如果一个城市的销售点小麦价格方差越大,则称其价格差异性越大.请你对A,B,C三个城市按照小麦价格差异性从大到小进行排序(只写出结果).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 是由正整数组成的无穷数列,对任意
是由正整数组成的无穷数列,对任意![]() ,
,![]() 满足如下两个条件:①
满足如下两个条件:①![]() 是
是![]() 的倍数;②
的倍数;②![]() .
.
(1)若![]() ,
,![]() ,写出满足条件的所有
,写出满足条件的所有![]() 的值;
的值;
(2)求证:当![]() 时,
时,![]() ;
;
(3)求![]() 所有可能取值中的最大值.
所有可能取值中的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1所示,在![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 为
为![]() 的平分线,点
的平分线,点![]() 在线段
在线段![]() 上,
上, ![]() .如图2所示,将
.如图2所示,将![]() 沿
沿![]() 折起,使得平面
折起,使得平面![]() 平面
平面![]() ,连结
,连结![]() ,设点
,设点![]() 是
是![]() 的中点.
的中点.

图1 图2
(1)求证: ![]() 平面
平面![]() ;
;
(2)在图2中,若![]() 平面
平面![]() ,其中
,其中![]() 为直线
为直线![]() 与平面
与平面![]() 的交点,求三棱锥
的交点,求三棱锥![]() 的体积.
的体积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com