练习册

  • 练习册
  • 试题
    相关习题
     0  230463  230471  230477  230481  230487  230489  230493  230499  230501  230507  230513  230517  230519  230523  230529  230531  230537  230541  230543  230547  230549  230553  230555  230557  230558  230559  230561  230562  230563  230565  230567  230571  230573  230577  230579  230583  230589  230591  230597  230601  230603  230607  230613  230619  230621  230627  230631  230633  230639  230643  230649  230657  266669 

    科目： 来源： 题型：选择题

    4．已知函数f（x）=sin（2x+θ），其中0＜θ＜2π，若x=$\frac{π}{6}$是函数的一条对称轴，且f（$\frac{π}{2}$）＞f（π），则θ等于（　　）
    A．$\frac{π}{6}$B．$\frac{5π}{6}$C．$\frac{7π}{6}$D．$\frac{11π}{6}$

    查看答案和解析>>

    科目： 来源： 题型：选择题

    3．复数$\frac{-3+i}{2+i}$=（　　）
    A．2+iB．2-iC．-1+iD．-1-i

    查看答案和解析>>

    科目： 来源： 题型：选择题

    2．直线$\sqrt{3}x$-y+a=0（a为常数）的斜率为（　　）
    A．$\frac{\sqrt{3}}{3}$B．$\sqrt{3}$C．-$\sqrt{3}$D．-$\frac{\sqrt{3}}{3}$

    查看答案和解析>>

    科目： 来源： 题型：解答题

    1．（1）$\frac{tan（π-a）•cos（2π-a）•sin（-a+\frac{3}{2}π）}{cos（-a-π）•sin（-π-a）}$．
    （2）tan70°cos10°（$\sqrt{3}$tan20°-1）．

    查看答案和解析>>

    科目： 来源： 题型：填空题

    20．已知向量$\overrightarrow{a}$，$\overrightarrow{b}$，其中|$\overrightarrow{a}$|=$\sqrt{2}$，|$\overrightarrow{b}$|=2，且（$\overrightarrow{a}$-$\overrightarrow{b}$）⊥$\overrightarrow{a}$，则|$\overrightarrow{2a}$-$\overrightarrow{b}$|=2．

    查看答案和解析>>

    科目： 来源： 题型：选择题

    19．若点（sin$\frac{5π}{6}$，cos$\frac{5π}{6}$）在角α的终边上，则角α的终边位于（　　）
    A．第一象限B．第二象限C．第三象限D．第四象限

    查看答案和解析>>

    科目： 来源： 题型：选择题

    18．若0＜α＜$\frac{π}{2}$，-π＜β＜-$\frac{π}{2}$，cos（$\frac{π}{4}$+α）=$\frac{1}{3}$，cos（$\frac{π}{4}$-$\frac{β}{2}$）=-$\frac{\sqrt{3}}{3}$，则cos（α+$\frac{β}{2}$）=（　　）
    A．-$\frac{5\sqrt{3}}{9}$B．$\frac{5\sqrt{3}}{9}$C．-$\frac{\sqrt{3}}{3}$D．$\frac{\sqrt{3}}{3}$

    查看答案和解析>>

    科目： 来源： 题型：解答题

    17．设平面直角坐标系xOy中，曲线G：y=$\frac{{x}^{2}}{2}$+$\frac{a}{2}$x-a2（x∈R），a为常数．
    （1）若a≠0，曲线G的图象与两坐标轴有三个交点，求经过这三个交点的圆C的一般方程；
    （2）在（1）的条件下，求圆心C所在曲线的轨迹方程；
    （3）若a=0，已知点M（0，3），在y轴上存在定点N（异于点M）满足：对于圆C上任一点P，都有$\frac{|PN|}{|PM|}$为一常数，试求所有满足条件的点N的坐标及该常数．

    查看答案和解析>>

    科目： 来源： 题型：解答题

    16．如图，平面ABCD⊥平面ADEF，四边形ABCD为菱形，四边形ADEF为矩形，M、N分别是EF、BC的中点，AB=2AF=2，∠CBA=60°．
    （1）求证：AN⊥DM；
    （2）求直线MN与平面ADEF所成的角的正切值；
    （3）求三棱锥D-MAN的体积．

    查看答案和解析>>

    科目： 来源： 题型：解答题

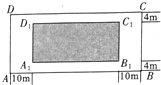    15．随着我市九龙江南岸江滨路建设的持续推进，未来市民将新增又一休闲好去处，据悉南江滨路建设工程规划配套建造一个长方形公园ABCD，如图所示，公园由长方形的休闲区A1B1C1D1（阴影部分）和环公园人行道组成，已知休闲区A1B1C1D1的面积为4000m2，人行道的宽度分别为4m和10m．
    （1）若休闲区的长A1B1=x m，求公园ABCD所占面积S关于x的函数S（x）的解析式；
    （2）要使公园所占面积最小，休闲区A1B1C1D1的长和宽该如何设计？

    查看答案和解析>>

    同步练习册答案