
科目: 来源: 题型:解答题
查看答案和解析>>
科目: 来源: 题型:解答题
查看答案和解析>>
科目: 来源: 题型:解答题
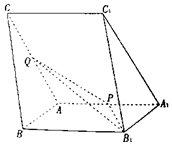 如图,三棱柱ABC-A1B1C1中,∠B1A1A=∠C1A1A=60°,AA1=AC=4,AB=2,P,Q分别为棱AA1,AC的中点.
如图,三棱柱ABC-A1B1C1中,∠B1A1A=∠C1A1A=60°,AA1=AC=4,AB=2,P,Q分别为棱AA1,AC的中点.查看答案和解析>>
科目: 来源: 题型:选择题
| A. | $\frac{π}{6}$个单位 | B. | $\frac{π}{3}$个单位 | C. | $\frac{π}{4}$个单位 | D. | $\frac{π}{12}$个单位 |
查看答案和解析>>
科目: 来源: 题型:填空题
查看答案和解析>>
科目: 来源: 题型:解答题
查看答案和解析>>
科目: 来源: 题型:选择题
| A. | 奇函数且在(-∞,+∞)上是增函数 | B. | 奇函数且在(-∞,+∞)上是减函数 | ||
| C. | 偶函数且在(-∞,+∞)上是增函数 | D. | 偶函数且在(-∞,+∞)上是减函数 |
查看答案和解析>>
科目: 来源: 题型:解答题
 某重点高中拟把学校打造成新型示范高中,为此制定了很多新的规章制度,新规章制度实施一段时间后,学校就新规章制度的认知程度随机抽取100名学生进行问卷调查,调查卷共有20个问题,每个问題5分,调查结束后,发现这100名学生的成绩都在[75,100]内,按成绩分成5组:第1组[75,80),第2组[80,85)第3组[85,90),第4组[90,95),第5组[95,100],绘制成如图所示的频率分布直方图,已知甲、乙、丙上分别在第3,4,5组,现在用分层抽样的方法在第3,4,5组共选取6人对新规取章制度作深入学习.
某重点高中拟把学校打造成新型示范高中,为此制定了很多新的规章制度,新规章制度实施一段时间后,学校就新规章制度的认知程度随机抽取100名学生进行问卷调查,调查卷共有20个问题,每个问題5分,调查结束后,发现这100名学生的成绩都在[75,100]内,按成绩分成5组:第1组[75,80),第2组[80,85)第3组[85,90),第4组[90,95),第5组[95,100],绘制成如图所示的频率分布直方图,已知甲、乙、丙上分别在第3,4,5组,现在用分层抽样的方法在第3,4,5组共选取6人对新规取章制度作深入学习.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com