10．已知向量m=.n=($2\sqrt{3}cosx.cos2x$).且函数f(x)=mn的最小正周期和取得最大值时自变量的取值集合,的图象向左平移$\frac{π}{12}$个单位.再将所得图象上——青夏教育精英家教网—

相关习题

0 250886 250894 250900 250904 250910 250912 250916 250922 250924 250930 250936 250940 250942 250946 250952 250954 250960 250964 250966 250970 250972 250976 250978 250980 250981 250982 250984 250985 250986 250988 250990 250994 250996 251000 251002 251006 251012 251014 251020 251024 251026 251030 251036 251042 251044 251050 251054 251056 251062 251066 251072 251080 266669

科目： 来源： 题型：解答题

10．已知向量m=（sinx，1），n=（$2\sqrt{3}cosx，cos2x$），且函数f（x）=mn
（1）求f（x）的最小正周期和取得最大值时自变量的取值集合；
（2）将函数y=f（x）的图象向左平移$\frac{π}{12}$个单位，再将所得图象上各点的横坐标缩短为原来的$\frac{1}{2}$，纵坐标不变，得到函数y=g（x）的图象．求g（x）在[0，$\frac{5π}{24}$]的值域．

查看答案和解析>>

科目： 来源： 题型：填空题

9．设函数$f（x）=\left\{{\begin{array}{l}{3x-1，x＜1}\\{{2^x}，x≥1}\end{array}}\right.$，则满足f（f（a））=2^f（a）的a的取值范围是[$\frac{2}{3}$，+∞）．

查看答案和解析>>

科目： 来源： 题型：填空题

8．已知$\overrightarrow{a}$=（-1，2），$\overrightarrow{b}$=（2，m），若$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为钝角，则m的取值范围是m＜1且m≠-4．

查看答案和解析>>

科目： 来源： 题型：选择题

7．设f（x）是定义域为R的偶函数，且对任意实数x，都有f（x+3π）=f（x），若$f（x）=\left\{{\begin{array}{l}{cosx，0≤x＜\frac{π}{2}}\\{sinx，\frac{π}{2}≤x≤\frac{3π}{2}}\end{array}}\right.$，则$f（{-\frac{17π}{4}}）$等于（　　）

A．

B．

$\frac{{\sqrt{2}}}{2}$

C．

$-\frac{{\sqrt{2}}}{2}$

D．

-1

查看答案和解析>>

科目： 来源： 题型：选择题

6．已知$sin（{\frac{π}{4}-α}）=\frac{5}{13}，α∈（0，\frac{π}{4}）$，则$\frac{cos2α}{{cos（{\frac{π}{4}+α}）}}$的值为（　　）

A．

$\frac{24}{13}$

B．

$-\frac{24}{13}$

C．

$\frac{10}{13}$

D．

$-\frac{10}{13}$

查看答案和解析>>

科目： 来源： 题型：解答题

5．

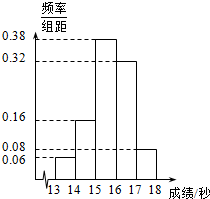2015年08月22日至2015年08月30日在北京举行国际田联世界田径锦标赛，其中50名运动员在一次百米测试中，成绩全部介于13秒与18秒之间，来自牙买加的运动员博尔特取得最好的成绩．将测试结果按如下方式分成五组：第一组[13，14），第二组[14，15）…第五组[17，18]，
如图是按上述分组方法得到的频率分布直方图
（1）若成绩大于或等于14秒且小于16秒的认为良好，求50名运动员在这次百米测试中成绩良好的人数；
（2）设m，n表示50名运动员中某两名运动员的百米测试成绩，且已知m，n∈[13，14）∪[17，18]，求事件“|m-n|＞1”的概率．

查看答案和解析>>

科目： 来源： 题型：填空题

4．已知$\left\{{\begin{array}{l}{2x+3y≤6}\\{x-y≥0}\\{y≥0}\end{array}}$则z=3x-y的最大值为9．

查看答案和解析>>

科目： 来源： 题型：选择题

3．已知直线l经过点M（2，3），当l截圆（x-2）²+（y+3）²=9所得弦长最长时，直线l的方程为（　　）

A．

x-2y+4=0

B．

3x+4y-18=0

C．

y+3=0