
科目: 来源: 题型:
【题目】对于函数![]() 有如下结论:
有如下结论:
①该函数为偶函数;
②若![]() ,则
,则![]() ;
;
③其单调递增区间是![]() ;
;
④值域是![]() ;
;
⑤该函数的图象与直线![]() 有且只有一个公共点.(本题中
有且只有一个公共点.(本题中![]() 是自然对数的底数)
是自然对数的底数)
其中正确的是__________.(请把正确结论的序号填在横线上)
查看答案和解析>>
科目: 来源: 题型:
【题目】已知方程![]() .
.
(1)求该方程表示一条直线的条件;
(2)当![]() 为何实数时,方程表示的直线斜率不存在?求出这时的直线方程;
为何实数时,方程表示的直线斜率不存在?求出这时的直线方程;
(3)已知方程表示的直线![]() 在
在![]() 轴上的截距为-3,求实数
轴上的截距为-3,求实数![]() 的值;
的值;
(4)若方程表示的直线![]() 的倾斜角是45°,求实数
的倾斜角是45°,求实数![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,点
中,点![]() ,直线
,直线![]() ,设圆
,设圆![]() 的半径为1,圆心在
的半径为1,圆心在![]() 上.
上.
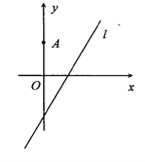
(1)若圆心![]() 也在直线
也在直线![]() 上,过点
上,过点![]() 作圆
作圆![]() 的切线,求切线的方程;
的切线,求切线的方程;
(2)若圆![]() 上存在点
上存在点![]() ,使
,使![]() ,求圆心
,求圆心![]() 的横坐标
的横坐标![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】4个男生,3个女生站成一排.(必须写出算式再算出结果才得分)
(Ⅰ)3个女生必须排在一起,有多少种不同的排法?
(Ⅱ)任何两个女生彼此不相邻,有多少种不同的排法?
(Ⅲ)甲乙二人之间恰好有三个人,有多少种不同的排法?
查看答案和解析>>
科目: 来源: 题型:
【题目】随着互联网的发展,移动支付(又称手机支付)越来越普通,某学校兴趣小组为了了解移动支付在大众中的熟知度,对15-65岁的人群随机抽样调查,调查的问题是“你会使用移动支付吗?”其中,回答“会”的共有![]() 个人.把这
个人.把这![]() 个人按照年龄分成5组:第1组
个人按照年龄分成5组:第1组![]() ,第2组
,第2组![]() ,第3组
,第3组![]() ,第4组
,第4组![]() ,第5组
,第5组![]() ,然后绘制成如图所示的频率分布直方图.其中,第一组的频数为20.
,然后绘制成如图所示的频率分布直方图.其中,第一组的频数为20.
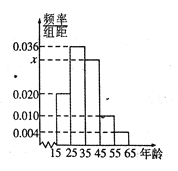
(1)求![]() 和
和![]() 的值,并根据频率分布直方图估计这组数据的众数;
的值,并根据频率分布直方图估计这组数据的众数;
(2)从第1,3,4组中用分层抽样的方法抽取6人,求第1,3,4组抽取的人数;
(3)在(2)抽取的6人中再随机抽取2人,求所抽取的2人来自同一个组的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】在三棱锥![]() 中,
中, ![]() 和
和![]() 是边长为
是边长为![]() 的等边三角形,
的等边三角形, ![]() ,
, ![]() 是
是![]() 中点,
中点, ![]() 是
是![]() 中点.
中点.
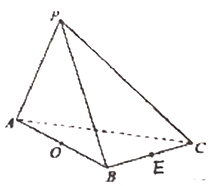
(Ⅰ)求证:平面![]() 平面
平面![]() ;
;
(Ⅱ)求直线![]() 与平面
与平面![]() 所成角的正弦值的大小;
所成角的正弦值的大小;
(Ⅲ)在棱![]() 上是否存在一点
上是否存在一点![]() ,使得
,使得![]() 的余弦值为
的余弦值为![]() ?若存在,指出点
?若存在,指出点![]() 在
在![]() 上的位置;若不存在,说明理由.
上的位置;若不存在,说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】某地拟建一座长为640米的大桥![]() ,假设桥墩等距离分布,经设计部门测算,两端桥墩
,假设桥墩等距离分布,经设计部门测算,两端桥墩![]() 造价总共为100万元,当相邻两个桥墩的距离为
造价总共为100万元,当相邻两个桥墩的距离为![]() 米时(其中
米时(其中![]() ).中间每个桥墩的平均造价为
).中间每个桥墩的平均造价为![]() 万元,桥面每1米长的平均造价为
万元,桥面每1米长的平均造价为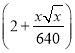 万元.
万元.

(1)试将桥的总造价表示为![]() 的函数
的函数![]() ;
;
(2)为使桥的总造价最低,试问这座大桥中间(两端桥墩![]() 除外)应建多少个桥墩?
除外)应建多少个桥墩?
查看答案和解析>>
科目: 来源: 题型:
【题目】若函数![]() 定义域为
定义域为![]() ,且对任意实数
,且对任意实数![]() ,有
,有![]() ,则称
,则称![]() 为“
为“![]() 形函数”,若函数
形函数”,若函数![]() 定义域为
定义域为![]() ,函数
,函数![]() 对任意
对任意![]() 恒成立,且对任意实数
恒成立,且对任意实数![]() ,有
,有![]() ,则称为“对数
,则称为“对数![]() 形函数” .
形函数” .
(1)试判断函数![]() 是否为“
是否为“![]() 形函数”,并说明理由;
形函数”,并说明理由;
(2)若![]() 是“对数
是“对数![]() 形函数”,求实数
形函数”,求实数![]() 的取值范围;
的取值范围;
(3)若![]() 是“
是“![]() 形函数”,且满足对任意
形函数”,且满足对任意![]() ,有
,有![]() ,问
,问![]() 是否为“对数
是否为“对数![]() 形函数”?证明你的结论.
形函数”?证明你的结论.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数![]() (
(![]() 为实数).
为实数).
(1)当![]() 时,求函数
时,求函数![]() 的图象在点
的图象在点![]() 处的切线方程;
处的切线方程;
(2)设函数![]() (其中
(其中![]() 为常数),若函数
为常数),若函数![]() 在区间
在区间![]() 上不存在极值,且存在
上不存在极值,且存在![]() 满
满
足![]() ,求
,求![]() 的取值范围;
的取值范围;
(3)已知![]() ,求证:
,求证:![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com