【题目】如图, 在△中, 点在边上, .

（Ⅰ）求；

（Ⅱ）若△的面积是, 求.

【题目】某厂有4台大型机器，在一个月中，一台机器至多出现1次故障，且每台机器是否出现故障是相互独立的，出现故障时需1名工人进行维修，每台机器出现故障需要维修的概率为.

(1)若出现故障的机器台数为，求的分布列；

(2) 该厂至少有多少名工人才能保证每台机器在任何时刻同时出现故障时能及时进行维修的概率不少于90%？

(3)已知一名工人每月只有维修1台机器的能力，每月需支付给每位工人1万元的工资，每台机器不出现故障或出现故障能及时维修，就使该厂产生5万元的利润，否则将不产生利润，若该厂现有2名工人，求该厂每月获利的均值.

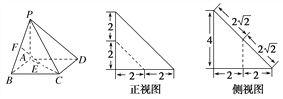
(1)求EF与平面ABCD所成角的大小；

(2)求二面角B－PA－C的大小.

在平面直角坐标系中，直线的参数方程是（为参数），以为极点， 轴的正半轴为极轴，建立极坐标系，曲线的极坐标方程为，且直线与曲线交于两点.

（Ⅰ）求曲线的直角坐标方程及直线恒过的定点的坐标；

（Ⅱ）在（Ⅰ）的条件下，若，求直线的普通方程.

【题目】已知函数的定义域是.

（1）判断在上的单调性，并证明；

（2）若不等式对任意恒成立，求实数的取值范围.

【题目】已知函数

(1)若函数的图象与x轴无交点，求a的取值范围；

(2) 若函数在[-1,1]上存在零点，求a的取值范围；

(3)设函数，当时，若对任意的，总存在，使得，求b的取值范围.

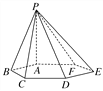
A. CD∥平面PAF

B. DF⊥平面PAF

C. CF∥平面PAB

D. CF⊥平面PAD

【题目】已知函数.

（1）证明：对任意的，函数的图像与直线最多有一个交点；

（2）设函数，若函数与函数的图像至少有一个交点，求实数的取值范围.

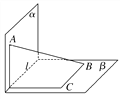
A. 30° B. 45°

C. 60° D. 75°

【题目】如图，已知底角为的等腰梯形，底边长为12，腰长为，当一条垂直于底边 (垂足为）的直线从左至右移动（与梯形有公共点）时，直线把梯形分成两部分.

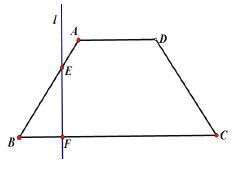
（1）令，试写出直线右边部分的面积与的函数解析式；

（2）在（1）的条件下，令.构造函数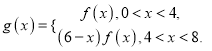

①判断函数在上的单调性；

②判断函数在定义域内是否具有单调性，并说明理由.