
科目: 来源: 题型:
【题目】在直角坐标系![]() 中,已知曲线
中,已知曲线![]() (
(![]() 为参数),在以
为参数),在以![]() 为极点,
为极点, ![]() 轴正半轴为极轴的极坐标系中,曲线
轴正半轴为极轴的极坐标系中,曲线![]() ,曲线
,曲线![]() .
.
(1)求曲线![]() 与
与![]() 的交点
的交点![]() 的直角坐标;
的直角坐标;
(2)设点![]() ,
, ![]() 分别为曲线
分别为曲线![]() 上的动点,求
上的动点,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目: 来源: 题型:
【题目】一张半径为4的圆形纸片的圆心为![]() ,
, ![]() 是圆内一个定点,且
是圆内一个定点,且![]() ,
, ![]() 是圆上一个动点,把纸片折叠使得
是圆上一个动点,把纸片折叠使得![]() 与
与![]() 重合,然后抹平纸片,折痕为
重合,然后抹平纸片,折痕为![]() ,设
,设![]() 与半径
与半径![]() 的交点为
的交点为![]() ,当
,当![]() 在圆上运动时,则
在圆上运动时,则![]() 点的轨迹为曲线
点的轨迹为曲线![]() ,以
,以![]() 所在直线
所在直线![]() 为轴,
为轴, ![]() 的中垂线为
的中垂线为![]() 轴建立平面直角坐标系,如图.
轴建立平面直角坐标系,如图.
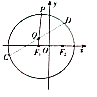
(1)求曲线![]() 的方程;
的方程;
(2)曲线![]() 与
与![]() 轴的交点为
轴的交点为![]() ,
, ![]() (
(![]() 在
在![]() 左侧),与
左侧),与![]() 轴不重合的动直线
轴不重合的动直线![]() 过点
过点![]() 且与
且与![]() 交于
交于![]() 、
、![]() 两点(其中
两点(其中![]() 在
在![]() 轴上方),设直线
轴上方),设直线![]() 、
、![]() 交于点
交于点![]() ,求证:动点
,求证:动点![]() 恒在定直线
恒在定直线![]() 上,并求
上,并求![]() 的方程.
的方程.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知![]() ,函数
,函数![]() .
.
(1)当![]() 时,解不等式
时,解不等式![]() ;
;
(2)若关于![]() 的方程
的方程![]() 的解集中恰有一个元素,求
的解集中恰有一个元素,求![]() 的值;
的值;
(3)设![]() ,若对任意
,若对任意![]() ,函数
,函数![]() 在区间
在区间![]() 上的最大值与最小值的差不超过1,求
上的最大值与最小值的差不超过1,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数f(x)=x2-3x+lnx.
(Ⅰ)求函数f(x)的极值;
(Ⅱ)若对于任意的x1,x2∈(1,+∞),x1≠x2,都有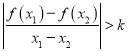 恒成立,求实数k的取值范围.
恒成立,求实数k的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知![]() 是抛物线
是抛物线![]() 的焦点,
的焦点, ![]() 为抛物线
为抛物线![]() 上不同的两点,
上不同的两点, ![]() 分别是抛物线
分别是抛物线![]() 在点
在点![]() 、点
、点![]() 处的切线,
处的切线, ![]() 是
是![]() 的交点.
的交点.
(1)当直线![]() 经过焦点
经过焦点![]() 时,求证:点
时,求证:点![]() 在定直线上;
在定直线上;
(2)若![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】为推行“新课堂”教学法,某化学老师分别用传统教学和“新课堂”两种不同的教学方式,在甲、乙两个平行班进行教学实验,为了解教学效果,期中考试后,分别从两个班级中各随机抽取![]() 名学生的成绩进行统计,作出的茎叶图如下图,记成绩不低于
名学生的成绩进行统计,作出的茎叶图如下图,记成绩不低于![]() 分者为“成绩优良”.
分者为“成绩优良”.
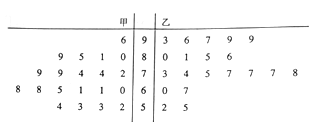
(1)分别计算甲、乙两班![]() 个样本中,化学分数前十的平均分,并据此判断哪种教学方式的教学效果更
个样本中,化学分数前十的平均分,并据此判断哪种教学方式的教学效果更
佳;
(2)甲、乙两班![]() 个样本中,成绩在
个样本中,成绩在![]() 分以下(不含
分以下(不含![]() 分)的学生中任意选取
分)的学生中任意选取![]() 人,求这
人,求这![]() 人来自不同班级的概率;
人来自不同班级的概率;
(3)由以上统计数据填写下面![]() 列联表,并判断能否在犯错误的概率不超过
列联表,并判断能否在犯错误的概率不超过![]() 的前提下认为“成绩优良与教学方式有关”?
的前提下认为“成绩优良与教学方式有关”?
甲班 | 乙班 | 总计 | |
成绩优良 | |||
成绩不优良 | |||
总计 |
附: 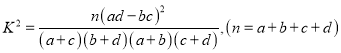
独立性检验临界值表:
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目: 来源: 题型:
【题目】数学课上,老师为了提高同学们的兴趣,先让同学们从1到3循环报数,结果最后一个同学报2;再让同学们从1到5循环报数,最后一个同学报3;又让同学们从1到7循报数,最后一个同学报4.请你设计一个算法,计算这个班至少有多少人,并画出程序框图.
查看答案和解析>>
科目: 来源: 题型:
【题目】为了解某班学生喜爱打篮球是否与性别有关,对本班50人进行了问卷调查得到了如下列表:
喜爱打篮球 | 不喜爱打篮球 | 合计 | |
男生 | 5 | ||
女生 | 10 | ||
合计 | 50 |
已知在全班50人中随机抽取1人,抽到喜爱打篮球的学生的概率为![]() .
.
(1)请将上表补充完整(不用写计算过程);
(2)能否有99.5%的把握认为喜爱打篮球与性别有关?说明你的理由.
下面的临界值表供参考:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(参考公式: 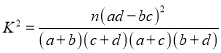 ,其中
,其中![]() )
)
查看答案和解析>>
科目: 来源: 题型:
【题目】下面程序的功能是( )
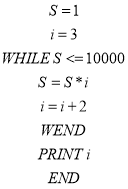
A. 求1×2×3×4×…×10 00的值
B. 求2×4×6×8×…×10 000的值
C. 求3×5×7×9×…×10 001的值
D. 求满足1×3×5×…×n>10 000的最小正整数n
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com