
科目: 来源: 题型:
【题目】已知函数f(x)=x+ ![]() (Ⅰ)判断函数的奇偶性,并加以证明;
(Ⅰ)判断函数的奇偶性,并加以证明;
(Ⅱ)用定义证明f(x)在(0,1)上是减函数;
(Ⅲ)函数f(x)在(﹣1,0)上是单调增函数还是单调减函数?(直接写出答案,不要求写证明过程).
查看答案和解析>>
科目: 来源: 题型:
【题目】共享单车的出现方便了人们的出行,深受我市居民的喜爱.为调查某校大学生对共享单车的使用情况,从该校8000名学生中按年级用分层抽样的方式随机抽取了100位同学进行调查,得到这100名同学每周使用共享单车的时间(单位:小时)如表:
使用时间 |
|
|
|
|
|
人数 | 10 | 40 | 25 | 20 | 5 |
(Ⅰ)已知该校大一学生由2400人,求抽取的100名学生中大一学生人数;
(Ⅱ)作出这些数据的频率分布直方图;
(Ⅲ)估计该校大学生每周使用共享单车的平均时间![]() (同一组中的数据用该组区间的中点值作代表).
(同一组中的数据用该组区间的中点值作代表).
查看答案和解析>>
科目: 来源: 题型:
【题目】全世界越来越关注环境保护问题,某监测站点于2016年8月某日起连续![]() 天监测空气质量指数
天监测空气质量指数![]() ,数据统计如下:
,数据统计如下:
空气质量指数 |
|
|
|
|
|
空气质量等级 | 空气优 | 空气良 | 轻度污染 | 中度污染 | 重度污染 |
天数 |
|
|
|
|
|
(1)根据所给统计表和频率分布直方图中的信息求出![]() 的值,并完成頻率分布直方图:
的值,并完成頻率分布直方图:
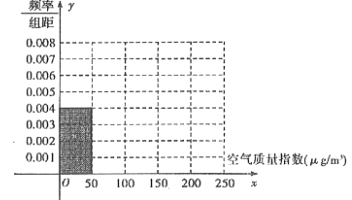
(2)由頻率分布直方图,求该组数据的平均数与中位数;
(3)在空气质量指数分别为![]() 和
和![]() 的监测数据中,用分层抽样的方法抽取
的监测数据中,用分层抽样的方法抽取![]() 天,从中任意选取
天,从中任意选取![]() 天,求事件
天,求事件![]() “两天空气都为良”发生的概率.
“两天空气都为良”发生的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】【2014高考课标2理数18】如图,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,
E为PD的中点.
(Ⅰ)证明:PB∥平面AEC;
(Ⅱ)设二面角D-AE-C为60°,AP=1,AD=![]() ,求三棱锥E-ACD的体积.
,求三棱锥E-ACD的体积.
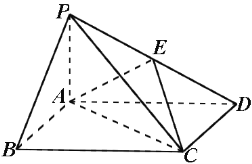
查看答案和解析>>
科目: 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的方程为
的方程为![]() ,直线
,直线![]() 的倾斜角为
的倾斜角为![]() 且经过点
且经过点![]() .
.
(1)以![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,求曲线
轴的正半轴为极轴建立极坐标系,求曲线![]() 的极坐标方程;
的极坐标方程;
(2)设直线![]() 与曲线
与曲线![]() 交于两点
交于两点![]() ,
,![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知△BCD中,∠BCD=90°,BC=CD=1,AB⊥平面BCD,∠ADB=60°,E、F分别是AC、AD上的动点,且![]()
(1)求证:不论![]() 为何值,总有平面BEF⊥平面ABC;
为何值,总有平面BEF⊥平面ABC;
(2)当λ为何值时,平面BEF⊥平面ACD ?

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线经过点A(0,4),B(1,0),C(5,0),其对称轴与x 轴相交于点M. 
(1)求抛物线的解析式和对称轴;
(2)在抛物线的对称轴上是否存在一点P,使△PAB的周长最小?若存在,请求出点P的坐标;若不存在,请说明理由;
(3)连结AC,在直线AC的下方的抛物线上,是否存在一点N,使△NAC的面积最大?若存在,请求出点N的坐标;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】【2017唐山模拟】如图,ABCDA1B1C1D1为正方体,连接BD,AC1,B1D1, CD1,B1C,现有以下几个结论:①BD∥平面CB1D1;②AC1⊥平面CB1D1;③AC1与底面ABCD所成角的正切值是;④CB1与BD为异面直线,其中所有正确结论的序号为________.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com