
科目: 来源: 题型:
【题目】已知椭圆C: ![]() =1(a>b>0)的右焦点为F2(1,0),点P(1,
=1(a>b>0)的右焦点为F2(1,0),点P(1, ![]() )在椭圆C上.
)在椭圆C上.
(1)求椭圆C的方程;
(2)过坐标原点O的两条直线EF,MN分别与椭圆C交于E,F,M,N四点,且直线OE,OM的斜率之积为﹣ ![]() ,求证:四边形EMFN的面积为定值.
,求证:四边形EMFN的面积为定值.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,PA⊥平面ABCD,AB⊥AD,AD∥BC,PA=AB=BC,AD=2AB,点M,N分别在PB,PC上,且MN∥BC. 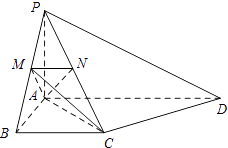
(1)证明:平面AMN⊥平面PBA;
(2)若M为PB的中点,求二面角M﹣AC﹣D的余弦值.
查看答案和解析>>
科目: 来源: 题型:
【题目】如表中给出了2011年~2015年某市快递业务总量的统计数据(单位:百万件)
年份 | 2011 | 2012 | 2013 | 2014 | 2015 |
年份代码 | 1 | 2 | 3 | 4 | 5 |
快递业务总量 | 34 | 55 | 71 | 85 | 105 |
(1)在图中画出所给数据的折线图; 
(2)建立一个该市快递量y关于年份代码x的线性回归模型;
(3)利用(2)所得的模型,预测该市2016年的快递业务总量.
附:回归直线方程的斜率和截距的最小二乘估计公式分别为:
斜率: 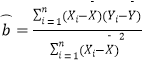 ,纵截距:
,纵截距: ![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】某学校高三年级有学生500人,其中男生300人,女生200人,为了研究学生的数学成绩是否与性别有关,现采用分层抽样的方法,从中抽取了100名学生,先统计了他们期中考试的数学分数,然后按性别分为男、女两组,再将两组学生的分数分成5组:[100,110),[110,120),[120,130),[130,140),[140,150]分别加以统计,得到如图所示的频率分布直方图.
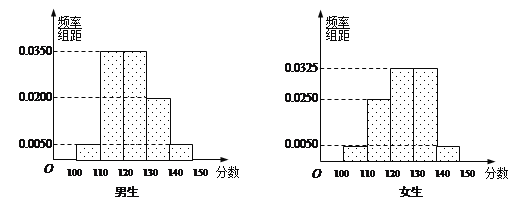
(1)从样本中分数小于110分的学生中随机抽取2人,求两人恰好为一男一女的概率;
(2)若规定分数不小于130分的学生为“数学尖子生”,请你根据已知条件完成2×2列联表,并判断是否有90%的把握认为“数学尖子生与性别有关”?
附:
P(K2≥k0) | 0.100 | 0.050 | 0.010 | 0.001 |
k0 | 2.706 | 3.841 | 6.635 | 10.828 |
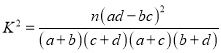 ,
,
查看答案和解析>>
科目: 来源: 题型:
【题目】给出下列四个命题:
①函数y=|x|与函数y= ![]() 表示同一个函数;
表示同一个函数;
②奇函数的图象一定通过直角坐标系的原点;
③函数y=3(x﹣1)2的图象可由y=3x2的图象向右平移1个单位得到;
④若函数f(x)的定义域为[0,2],则函数f(2x)的定义域为[0,4];
⑤设函数f(x)是在区间[a.b]上图象连续的函数,且f(a)f(b)<0,则方程f(x)=0在区间[a,b]上至少有一实根.
其中正确命题的序号是 . (填上所有正确命题的序号)
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在四棱锥![]() 中,AE⊥DE,CD⊥平面ADE,AB⊥平面ADE,CD=DA=6,AB=2,DE=3.
中,AE⊥DE,CD⊥平面ADE,AB⊥平面ADE,CD=DA=6,AB=2,DE=3.
(1)求![]() 到平面
到平面![]() 的距离
的距离
(2)在线段![]() 上是否存在一点
上是否存在一点![]() ,使
,使![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com