
科目: 来源: 题型:
【题目】从某学校高三年级共800名男生中随机抽取50人测量身高.数据表明,被测学生身高全部介于155cm到195cm之间,将测量结果按如下方式分成八组:第一组[155,160);第二组[160,165);…;第八组[190,195].如图是按上述分组方法得到的频率分布直方图的一部分.已知第一组与第八组人数相同,第六组比第七组少1人. 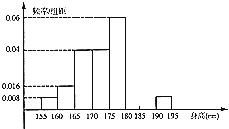
(1)估计这所学校高三年级全体男生身高在180cm以上(含180cm)的人数;
(2)若从身高属于第六组和第八组的所有男生中随机抽取两人,记他们的身高分别为x,y,求满足“|x﹣y|≤5”的事件的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知椭圆![]()
![]() 的离心率为
的离心率为![]() ,其左、右焦点分别为
,其左、右焦点分别为![]() ,左、右顶点分别为
,左、右顶点分别为![]() ,上、下顶点分别为
,上、下顶点分别为![]() ,四边形
,四边形![]() 与四边形
与四边形![]() 的面积之和为4.
的面积之和为4.
(1)求椭圆![]() 的方程;
的方程;
(2)直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,
两点,![]() (其中
(其中![]() 为坐标原点),求直线
为坐标原点),求直线![]() 被以线段
被以线段![]() 为直径的圆截得的弦长.
为直径的圆截得的弦长.
查看答案和解析>>
科目: 来源: 题型:
【题目】为大力提倡“厉行节俭,反对浪费”,某高中通过随机询问100名性别不同的学生是否做到“光盘”行动,得到如表所示联表及附表:
做不到“光盘”行动 | 做到“光盘”行动 | |
男 | 45 | 10 |
女 | 30 | 15 |
P(K2≥k0) | 0.10 | 0.05 | 0.025 |
k0 | 2.706 | 3.841 | 5.024 |
经计算:K2= ![]() ≈3.03,参考附表,得到的正确结论是( )
≈3.03,参考附表,得到的正确结论是( )
A.有95%的把握认为“该学生能否做到光盘行到与性别有关”
B.有95%的把握认为“该学生能否做到光盘行到与性别无关”
C.有90%的把握认为“该学生能否做到光盘行到与性别有关”
D.有90%的把握认为“该学生能否做到光盘行到与性别无关”
查看答案和解析>>
科目: 来源: 题型:
【题目】设函数f(x)=x2+aln(x+1).
(1)求函数f(x)的单调区间;
(2)若函数F(x)=f(x)+ln ![]() 有两个极值点x1 , x2且x1<x2 , 求证F(x2)>
有两个极值点x1 , x2且x1<x2 , 求证F(x2)> ![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】某搜索引擎广告按照付费价格对搜索结果进行排名,点击一次付费价格排名越靠前,被点击的次数也可能会提高,已知某关键词被甲、乙等多个公司竞争,其中甲、乙付费情况与每小时点击量结果绘制成如下的折线图.

(1)试根据所给数据计算每小时点击次数的均值方差并分析两组数据的特征;
(2)若把乙公司设置的每次点击价格为x,每小时点击次数为![]() ,则点
,则点![]() 近似在一条直线附近.试根据前5次价格与每小时点击次数的关系,求y关于x的回归直线
近似在一条直线附近.试根据前5次价格与每小时点击次数的关系,求y关于x的回归直线![]() .(附:回归方程系数公式:
.(附:回归方程系数公式: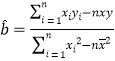 ,
,![]() ).
).
查看答案和解析>>
科目: 来源: 题型:
【题目】已知椭圆Γ: ![]() +
+ ![]() =1(a>b>0)的右焦点与短轴两端点构成一个面积为2的等腰直角三角形,O为坐标原点:
=1(a>b>0)的右焦点与短轴两端点构成一个面积为2的等腰直角三角形,O为坐标原点: 
(1)求椭圆Г的方程:
(2)设点A在椭圆Г上,点B在直线y=2上,且OA⊥OB,求证: ![]() +
+ ![]() 为定值:
为定值:
(3)设点C在Γ上运动,OC⊥OD,且点O到直线CD距离为常数d(0<d<2),求动点D的轨迹方程:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com