
【题目】设函数f(x)=x2+aln(x+1).
(1)求函数f(x)的单调区间;
(2)若函数F(x)=f(x)+ln ![]() 有两个极值点x1 , x2且x1<x2 , 求证F(x2)>
有两个极值点x1 , x2且x1<x2 , 求证F(x2)> ![]() .
.
【答案】
(1)解:函数f(x)的定义域为(﹣1,+∞),
![]() =
= ![]() ,(x>﹣1),
,(x>﹣1),
令g(x)=2x2+2x+a,则△=4﹣8a.
①当△<0,即a> ![]() 时,g(x)>0,从而f′(x)>0,
时,g(x)>0,从而f′(x)>0,
故函数f(x)在(﹣1,+∞)上单调递增;
②当△=0,即a= ![]() 时,g(x)≥0,此时f′(x)≥0,此时f′(x)在f′(x)=0的左右两侧不变号,
时,g(x)≥0,此时f′(x)≥0,此时f′(x)在f′(x)=0的左右两侧不变号,
故函数f(x)在(﹣1,0)上单调递增;
③当△>0,即a< ![]() 时,g(x)=0的两个根为
时,g(x)=0的两个根为 ![]() ,
, ![]() ,
,
当 ![]() ,即a≤0时,x1≤﹣1,当0<a<
,即a≤0时,x1≤﹣1,当0<a< ![]() 时,x1>﹣1.
时,x1>﹣1.
故当a≤0时,函数f(x)在(﹣1, ![]() )单调递减,在(
)单调递减,在( ![]() ,+∞)单调递增;
,+∞)单调递增;
当0<a< ![]() 时,函数f(x)在(﹣1,
时,函数f(x)在(﹣1, ![]() ),(
),( ![]() ,+∞)单调递增,
,+∞)单调递增,
在( ![]() ,
, ![]() )单调递减.
)单调递减.
(2)解:∵F(x)=f(x)+ln ![]() ,∴F′(x)=f′(x),
,∴F′(x)=f′(x),
∴当函数F(x)有两个极值点时0<a< ![]() ,0<
,0< ![]() <1,
<1,
故此时x2= ![]() ∈(﹣
∈(﹣ ![]() ,0),且g(x2)=0,即a=﹣(2
,0),且g(x2)=0,即a=﹣(2 ![]() +2x2),
+2x2),
∴F(x2)= ![]() +aln(1+x2)+ln
+aln(1+x2)+ln ![]()
= ![]() ﹣(
﹣( ![]() )ln(1+x2)+ln
)ln(1+x2)+ln ![]() ,
,
设h(x)=x2﹣(2x2+2x)ln(1+x)+ln ![]() ,其中﹣
,其中﹣ ![]() ,
,
则h′(x)=2x﹣2(2x+1)ln(1+x)﹣2x=﹣2(2x+1)ln(1+x),
由于﹣ ![]() 时,h′(x)>0,
时,h′(x)>0,
故函数h(x)在(﹣ ![]() ,0)上单调递增,
,0)上单调递增,
故h(x).h(﹣ ![]() )=
)= ![]() .
.
∴F(x2)=h(x2)> ![]() .
.
【解析】(1)由函数f(x)的定义域为(﹣1,+∞), ![]() =
= ![]() ,令g(x)=2x2+2x+a,则△=4﹣8a.由根的判断式进行分类讨论,能求出函数f(x)的单调区间.(2)由F′(x)=f′(x),知函数F(x)有两个极值点时,0<a<
,令g(x)=2x2+2x+a,则△=4﹣8a.由根的判断式进行分类讨论,能求出函数f(x)的单调区间.(2)由F′(x)=f′(x),知函数F(x)有两个极值点时,0<a< ![]() ,0<
,0< ![]() <1,由此推导出x2=
<1,由此推导出x2= ![]() ∈(﹣
∈(﹣ ![]() ,0),且g(x2)=0,即a=﹣(2
,0),且g(x2)=0,即a=﹣(2 ![]() +2x2),F(x2)=
+2x2),F(x2)= ![]() ﹣(
﹣( ![]() )ln(1+x2)+ln
)ln(1+x2)+ln ![]() ,构造函数h(x)=x2﹣(2x2+2x)ln(1+x)+ln
,构造函数h(x)=x2﹣(2x2+2x)ln(1+x)+ln ![]() ,能够证明F(x2)>
,能够证明F(x2)> ![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】函数f(x)= ![]() +lnx,其中a为实常数.
+lnx,其中a为实常数.
(1)讨论f(x)的单调性;
(2)不等式f(x)≥1在x∈(0,1]上恒成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,曲线C1的参数方程为 ![]() (θ为参数).以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C2的极坐标方程为ρcosθ=﹣2.
(θ为参数).以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C2的极坐标方程为ρcosθ=﹣2.
(1)求C1和C2在直角坐标系下的普通方程;
(2)已知直线l:y=x和曲线C1交于M,N两点,求弦MN中点的极坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆C1:(x﹣1)2+(y﹣3)2=1,圆C2:(x﹣6)2+(y﹣1)2=1,M,N分别是圆C1 , C2上的动点,P为直线x﹣y﹣2=0上的动点,则||PM|﹣|PN||的最大值为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,正三棱柱![]() 中,
中,![]() 为
为![]() 中点,
中点,![]() 为
为![]() 上的一点,
上的一点,![]() .
.
(1)若![]() 平面
平面![]() ,求证:
,求证:![]() .
.
(2)平面![]() 将棱柱
将棱柱![]() 分割为两个几何体,记上面一个几何体的体积为
分割为两个几何体,记上面一个几何体的体积为![]() ,下面一个几何体的体积为
,下面一个几何体的体积为![]() ,求
,求![]() .
.
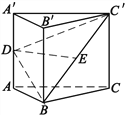
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从某学校高三年级共800名男生中随机抽取50人测量身高.数据表明,被测学生身高全部介于155cm到195cm之间,将测量结果按如下方式分成八组:第一组[155,160);第二组[160,165);…;第八组[190,195].如图是按上述分组方法得到的频率分布直方图的一部分.已知第一组与第八组人数相同,第六组比第七组少1人. 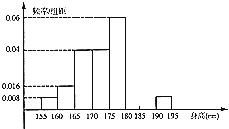
(1)估计这所学校高三年级全体男生身高在180cm以上(含180cm)的人数;
(2)若从身高属于第六组和第八组的所有男生中随机抽取两人,记他们的身高分别为x,y,求满足“|x﹣y|≤5”的事件的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和Sn=2n2+n,n∈N* .
(1)求{an}的通项公式;
(2)若数列{bn}满足an=4log2bn+3,n∈N* , 求数列{anbn}的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知⊙O是△ABC的外接圆,AB=BC,AD是BC边上的高,AE是⊙O的直径. 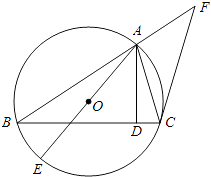
(1)求证:ACBC=ADAE;
(2)过点C作⊙O的切线交BA的延长线于点F,若AF=4,CF=6,求AC的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设集合A={(x,y)|(x﹣4)2+y2=1},B={(x,y)|(x﹣t)2+(y﹣at+2)2=1},如果命题“t∈R,A∩B≠”是真命题,则实数a的取值范围是( )
A.[1,4]
B.[0, ![]() ]
]
C.[0, ![]() ]
]
D.(﹣∞,0]∪( ![]() ,+∞]
,+∞]
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com