
科目: 来源: 题型:
【题目】【2017福建三明5月质检】已知直线![]() 与抛物线
与抛物线![]() 相切,且与
相切,且与![]() 轴的交点为
轴的交点为![]() ,点
,点![]() .若动点
.若动点![]() 与两定点
与两定点![]() 所构成三角形的周长为6.
所构成三角形的周长为6.
(Ⅰ) 求动点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(Ⅱ) 设斜率为![]() 的直线
的直线![]() 交曲线
交曲线![]() 于
于![]() 两点,当
两点,当![]() ,且
,且![]() 位于直线
位于直线![]() 的两侧时,证明:
的两侧时,证明: ![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】【2017广东佛山二模】已知椭圆![]() :
: ![]() (
(![]() )的焦距为4,左、右焦点分别为
)的焦距为4,左、右焦点分别为![]() 、
、![]() ,且
,且![]() 与抛物线
与抛物线![]() :
: ![]() 的交点所在的直线经过
的交点所在的直线经过![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)过![]() 的直线
的直线![]() 与
与![]() 交于
交于![]() ,
, ![]() 两点,与抛物线
两点,与抛物线![]() 无公共点,求
无公共点,求![]() 的面积的取值范围.
的面积的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知数列{an}的前n项和Sn满足2Sn=3an﹣3,数列{bn}的前n项和Tn满足 ![]() =
= ![]() +1且b1=1.
+1且b1=1.
(1)求数列{an},{bn}的通项公式;
(2)设cn= ![]() ,求数列{cn}的前n项和Pn;
,求数列{cn}的前n项和Pn;
(3)数列{Sn}中是否存在不同的三项Sp , Sq , Sr , 使这三项恰好构成等差数列?若存在,求出p,q,r的关系;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】实验杯足球赛采用七人制淘汰赛规则,某场比赛中一班与二班在常规时间内战平,直接进入点球决胜环节,在点球决胜环节中,双方首先轮流罚点球三轮,罚中更多点球的球队获胜;若双方在三轮罚球中未分胜负,则需要进行一对一的点球决胜,即双方各派处一名队员罚点球,直至分出胜负;在前三轮罚球中,若某一时刻胜负已分,尚未出场的队员无需出场罚球(例如一班在先罚球的情况下,一班前两轮均命中,二班前两轮未能命中,则一班、二班的第三位同学无需出场).由于一班同学平时踢球热情较高,每位队员罚点球的命中率都能达到0.8,而二班队员的点球命中串只有0.5,比赛时通过抽签决定一班在每一轮都先罚球.
(1)定义事件![]() 为“一班第三位同学没能出场罚球”,求事件
为“一班第三位同学没能出场罚球”,求事件![]() 发生的概率;
发生的概率;
(2)若两队在前三轮点球结束后打平,则进入一对一点球决胜,一对一球决胜由没有在之前点球大战中出场过的队员主罚点球,若在一对一点球决胜的某一轮中,某对队员射入点球且另一队员未能射入,则比赛结束;若两名队员均射入或者均射失点球,则进行下一轮比赛. 若直至双方场上每名队员都已经出场罚球,则比赛亦结束,双方通过抽签决定胜负,本场比赛中若已知双方在点球大战,以随机变量![]() 记录双方进行一对一点球决胜的轮数,求
记录双方进行一对一点球决胜的轮数,求![]() 的分布列与数学期望.
的分布列与数学期望.
查看答案和解析>>
科目: 来源: 题型:
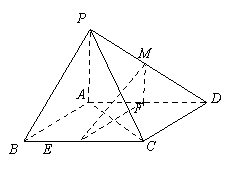
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 是平行四边形,
是平行四边形,![]() ,侧面
,侧面![]() 底面
底面![]() ,
,![]() ,
,![]() ,
, ![]() 分别为
分别为![]() 的中点,点
的中点,点![]() 在线段
在线段![]() 上.
上.
(Ⅰ)求证:![]() 平面
平面![]() ;
;
(Ⅱ)如果直线![]() 与平面
与平面![]() 所成的角和直线
所成的角和直线![]() 与平面
与平面![]() 所成的角相等,求
所成的角相等,求![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),在极坐标系(与直角坐标系
为参数),在极坐标系(与直角坐标系![]() 取相同的长度单位,且以原点
取相同的长度单位,且以原点![]() 为极点,以
为极点,以![]() 轴正半轴为极轴)中,圆
轴正半轴为极轴)中,圆![]() 的方程为
的方程为![]() .
.
(1)求圆![]() 的直角坐标方程;
的直角坐标方程;
(2)设圆![]() 与直线
与直线![]() 交于点
交于点![]() ,若点
,若点![]() 的坐标为
的坐标为![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知直线l:y=x+1,圆O: ![]() ,直线l被圆截得的弦长与椭圆C:
,直线l被圆截得的弦长与椭圆C: ![]() 的短轴长相等,椭圆的离心率e=
的短轴长相等,椭圆的离心率e= ![]() .
.
(1)求椭圆C的方程;
(2)过点M(0, ![]() )的动直线l交椭圆C于A、B两点,试问:在坐标平面上是否存在一个定点T,使得无论l如何转动,以AB为直径的圆恒过定点T?若存在,求出点T的坐标;若不存在,请说明理由.
)的动直线l交椭圆C于A、B两点,试问:在坐标平面上是否存在一个定点T,使得无论l如何转动,以AB为直径的圆恒过定点T?若存在,求出点T的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com