【题目】已知{an}是首项为a1 ， 公比为q的等比数列，Sn是{an}的前n项和．Sn= ；若am+an=as+at ， 则m+n=s+t；Sk ， S2k﹣Sk ， S3k﹣S2k成等比数列（k∈N）．
以上说法正确的有（ ）个．
A.0
B.1
C.2
D.3

【题目】在正方体ABCD﹣A1B1C1D1中，动点P在底面ABCD内，且P到棱AD的距离与到面对角线BC1的距离相等，则点P的轨迹是（　　）
A.线段
B.椭圆的一部分
C.双曲线的一部分
D.抛物线的一部分

【题目】执行如图所示的程序框图，输出S的值为（ ）

A.14
B.20
C.30
D.55

（1）当时，试判断四边形MNPE的形状，并求其面积；

（2）若使裁剪得到的四边形MNPE面积最大，请给出裁剪方案，并说明理由。

【题目】已知二次函数f（x）=x2+bx+c（其中b，c为实常数）．
（1）若b＞2，且y=f（sinx）（x∈R）的最大值为5，最小值为﹣1，求函数y=f（x）的解析式；
（2）是否存在这样的函数y=f（x），使得{y|y=x2+bx+c，﹣1≤x≤0}=[﹣1，0]，若存在，求出函数y=f（x）的解析式；若不存在，请说明理由．
（3）记集合A={x|f（x）=x，x∈R}，B={x|f（f（x））=x，x∈R}．
①若A≠，求证：B≠；
②若A=，判断B是否也为空集．

【题目】如图，点P、Q、R、S分别在正方体的四条棱上，并且是所在棱的中点，则直线PQ与RS是异面直线的一个图是（　　）
A.
B.
C.
D.

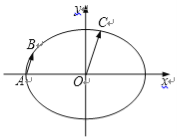
如图，在平面直角坐标系中，已知椭圆的离心率为，C为椭

圆上位于第一象限内的一点．

（1）若点的坐标为，求a，b的值；

（2）设A为椭圆的左顶点，B为椭圆上一点，且，求直线AB的斜率．

【题目】【苏北四市2016-2017学年度高三年级第一学期期末调研】如图，在平面直角坐标系中，已知椭圆的离心率为，且右焦点到左准线的距离为．

（1）求椭圆的标准方程；

（2）设为椭圆的左顶点，为椭圆上位于轴上方的点，直线交轴于点

，过点作的垂线，交轴于点．

（ⅰ）当直线的斜率为时，求的外接圆的方程；

（ⅱ）设直线交椭圆于另一点，求的面积的最大值．

【题目】如图，设圆弧x2+y2=1（x≥0，y≥0）与两坐标轴正半轴围成的扇形区域为M，过圆弧上中点A做该圆的切线与两坐标轴正半轴围成的三角形区域为N．现随机在区域N内投一点B，若设点B落在区域M内的概率为P，则P的值为（　　）

A.
B.
C.
D.

【题目】【南通市、泰州市2017届高三第一次调研测试】（本题满分14分）如图，在平面直角坐标系中，已知椭圆的离心率为，焦点到相应准线的距离为1.

（1）求椭圆的标准方程；

（2）若P为椭圆上的一点，过点O作OP的垂线交直线

于点Q，求的值；