
科目: 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为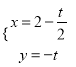 ,(
,( ![]() 为参数),在以坐标原点为极点,
为参数),在以坐标原点为极点, ![]() 轴正半轴为极轴的极坐标系中,曲线
轴正半轴为极轴的极坐标系中,曲线![]() 的极坐标方程为
的极坐标方程为![]()
(Ⅰ)求直线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)已知点![]() ,若点
,若点![]() 是直线
是直线![]() 上一动点,过点
上一动点,过点![]() 作曲线
作曲线![]() 的两条切线,切点分别为
的两条切线,切点分别为![]() ,求四边形
,求四边形![]() 面积的最小值.
面积的最小值.
查看答案和解析>>
科目: 来源: 题型:
【题目】下列四种说法正确的是( )
①函数f(x)的定义域是R,则“x∈R,f(x+1)>f(x)”是“函数f(x)为增函数”的充要条件
②命题“x∈R,( ![]() )x>0”的否定是“x∈R,(
)x>0”的否定是“x∈R,( ![]() )x≤0”
)x≤0”
③命题“若x=2,则x2﹣3x+2=0”的逆否命题是“若x2﹣3x+2≠0,则x≠2”
④p:在△ABC中,若cos2A=cos2B,则A=B;q:y=sinx在第一象限是增函数.则p∧q为真命题.
A.①②③④
B.①③
C.①③④
D.③
查看答案和解析>>
科目: 来源: 题型:
【题目】某投资公司现提供两种一年期投资理财方案,一年后投资盈亏的情况如下表:
投资股市 | 获利 | 不赔不赚 | 亏损 | 购买基金 | 获利 | 不赔不赚 | 亏损 | |
概率 |
|
|
| 概率 |
|
|
|
(Ⅰ)甲、乙两人在投资顾问的建议下分别选择“投资股市”和“买基金”,若一年后他们中至少有一人盈利的概率大于![]() ,求
,求![]() 的取值范围;
的取值范围;
(Ⅱ)若![]() ,某人现有
,某人现有![]() 万元资金,决定在“投资股市”和“购买基金”这两种方案中选择出一种,那么选择何种方案可使得一年后的投资收益的数学期望值较大.
万元资金,决定在“投资股市”和“购买基金”这两种方案中选择出一种,那么选择何种方案可使得一年后的投资收益的数学期望值较大.
查看答案和解析>>
科目: 来源: 题型:
【题目】若二次函数f(x)=ax2+bx+c(a,b,c∈R)满足f(x+1)﹣f(x)=4x+1,且f(0)=3.
(1)求f(x)的解析式;
(2)若在区间[﹣1,1]上,不等式f(x)>6x+m恒成立,求实数m的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知圆![]() ,定点
,定点![]() 为圆上一动点,线段
为圆上一动点,线段![]() 的垂直平分线交线段
的垂直平分线交线段![]() 于点
于点![]() ,设点
,设点![]() 的轨迹为曲线
的轨迹为曲线![]() ;
;
(Ⅰ)求曲线![]() 的方程;
的方程;
(Ⅱ)若经过![]() 的直线
的直线![]() 交曲线于不同的两点
交曲线于不同的两点![]() ,(点
,(点![]() 在点
在点![]() ,
, ![]() 之间),且满足
之间),且满足![]() ,求直线
,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目: 来源: 题型:
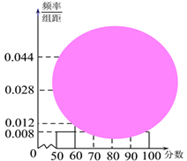
【题目】某校高一(1)班的一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的污损,可见部分如下图:
![]() 求分数在
求分数在![]() 的频率及全班人数;
的频率及全班人数;
![]() 求分数在
求分数在![]() 之间的频数,并计算频率分布直方图中
之间的频数,并计算频率分布直方图中![]() 间矩形的高;
间矩形的高;
![]() 若要从分数在
若要从分数在![]() 之间的试卷中任取两份分析学生失分情况,求在抽取的试卷中,至少有一份分数在
之间的试卷中任取两份分析学生失分情况,求在抽取的试卷中,至少有一份分数在![]() 之间的概率.
之间的概率.

查看答案和解析>>
科目: 来源: 题型:
【题目】设f(x)=aex+ ![]() +b(a>0).
+b(a>0).
(1)求f(x)在[0,+∞)上的最小值;
(2)设曲线y=f(x)在点(2,f(2))的切线方程为3x﹣2y=0,求a、b的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】红队队员甲、乙、丙与蓝队队员A、B、C进行围棋比赛,甲对A,乙对B,丙对C各一盘,已知甲胜A,乙胜B,丙胜C的概率分别为0.6,0.5,0.5,假设各盘比赛结果相互独立.
(1)求红队至少两名队员获胜的概率;
(2)用ξ表示红队队员获胜的总盘数,求ξ的分布列和数学期望Eξ.
查看答案和解析>>
科目: 来源: 题型:
【题目】国庆期间,某旅行社组团去风景区旅游,若旅行团人数在30人或30人以下,每人需交费用为900元;若旅行团人数多于30人,则给予优惠:每多1人,人均费用减少10元,直到达到规定人数75人为止.旅行社需支付各种费用共计15000元.
(1)写出每人需交费用y关于人数x的函数;
(2)旅行团人数为多少时,旅行社可获得最大利润?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com