【题目】已知幂函数f（x）=（m2﹣5m+7）x﹣m﹣1（m∈R）为偶函数．
（1）求 的值；
（2）若f（2a+1）=f（a），求实数a的值．

【题目】已知椭圆的焦距为，且过点.

（1）求椭圆的方程；

（2）若不经过点的直线与交于两点，且直线与直线的斜率之和为，证明：直线的斜率为定值.

【题目】化简或求值：
（1）（2 ）0+2﹣2×（2 ） ﹣（ ）
（2）2（lg ）2+lg lg5+ ．

【题目】如图，四棱锥中，侧面为等边三角形且垂直于底面，

.

（1）证明： ；

（2）若直线与平面所成角为，求二面角的余弦值.

在直线坐标系中，以坐标原点为极点， 轴正半轴为极轴建立极坐标系，直线的参数方程为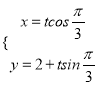（为参数），曲线的极坐标方程为.

（1）直线的普通方程和曲线的参数方程；

（2）设点在上， 在处的切线与直线垂直，求的直角坐标.

【题目】已知集合A={x|x＞1}，集合B={x|m≤x≤m+3}；
（1）当m=﹣1时，求A∩B，A∪B；
（2）若BA，求m的取值范围．

【题目】已知椭圆C： =1（a＞b＞0）过点A（﹣ ， ），离心率为 ，点F1 ， F2分别为其左右焦点．
（1）求椭圆C的标准方程；
（2）若y2=4x上存在两个点M，N，椭圆上有两个点P，Q满足，M，N，F2三点共线，P，Q，F2三点共线，且PQ⊥MN．求四边形PMQN面积的最小值．

（1）试分别估计芯片甲，芯片乙为合格品的概率；
（2）生产一件芯片甲，若是合格品可盈利40元，若是次品则亏损5元；生产一件芯片乙，若是合格品可盈利50元，若是次品则亏损10元．在（1）的前提下，记X为生产1件芯片甲和1件芯片乙所得的总利润，求随机变量X的分布列及生产1件芯片甲和1件芯片乙所得总利润的平均值．

【题目】 某厂生产不同规格的一种产品，根据检测标准，其合格产品的质量与尺寸之间近似满足关系式（为大于的常数），现随机抽取件合格产品，测得数据如下：

对数据作了初步处理，相关统计量的值如下表：

（1）根据所给数据，求关于的回归方程；

（2）按照某项指标测定，当产品质量与尺寸的比在区间内时为优等品，现从抽取的件合格产品中再任选件，记为取到优等品的件数，试求随机变量的分布列和期望.

附：对于一组数据，其回归直线的斜率和截距的最小二乘估计分别为.

【题目】已知函数．

（Ⅰ）若函数有零点，其实数的取值范围．

（Ⅱ）证明：当时， ．