
科目: 来源: 题型:
【题目】第26届世界大学生夏季运动会将于2011年8月12日到23日在深圳举行 ,为了搞好接待工作,组委会在某学院招募了12名男志愿者和18名女志愿者。将这30名志愿者的身高编成如右所示的茎叶图(单位:cm):

若身高在175cm以上(包括175cm)定义为“高个子”,身高在175cm以下(不包括175cm)定义为“非高个子”,且只有“女高个子”才担任“礼仪小姐”。
(1)如果用分层抽样的方法从“高个子”和“非高个子”中提取5人,再从这5人中选2人,那么至少有一人是“高个子”的概率是多少?
(2)若从所有“高个子”中选3名志愿者,用![]() 表示所选志愿者中能担任“礼仪小姐”的人数,试写出
表示所选志愿者中能担任“礼仪小姐”的人数,试写出![]() 的分布列,并求
的分布列,并求![]() 的数学期望。
的数学期望。
查看答案和解析>>
科目: 来源: 题型:
【题目】已知椭圆C中心在原点,焦点在坐标轴上,且该椭圆经过点( ![]() ,
, ![]() )和点
)和点 ![]() .求
.求
(1)椭圆C的方程;
(2)P,Q,M,N四点在椭圆C上,F1为负半轴上的焦点,直线PQ,MN都过F1且 ![]() ,求四边形PMQN的面积最小值和最大值.
,求四边形PMQN的面积最小值和最大值.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知正方形ABCD的边长为6,点E,F分别在边AB,AD上,AE=AF=4,现将△AEF沿线段EF折起到△A′EF位置,使得A′C=2 ![]() .
. 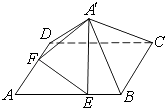
(1)求五棱锥A′﹣BCDFE的体积;
(2)求平面A′EF与平面A′BC的夹角.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数f(x)=ax2+(a﹣2)x﹣2,a∈R.
(1)若关于x的不等式f(x)≤0的解集为[﹣1,2],求实数a的值;
(2)当a<0时,解关于x的不等式f(x)≤0.
查看答案和解析>>
科目: 来源: 题型:
【题目】某学校为了解学校食堂的服务情况,随机调查了50名就餐的教师和学生.根据这50名师生对餐厅服务质量进行评分,绘制出了频率分布直方图(如图所示),其中样本数据分组为[40,50),[50,60),…,[90,100]. 
(1)求频率分布直方图中a的值;
(2)从评分在[40,60)的师生中,随机抽取2人,求此人中恰好有1人评分在[40,50)上的概率;
(3)学校规定:师生对食堂服务质量的评分不得低于75分,否则将进行内部整顿,试用组中数据估计该校师生对食堂服务质量评分的平均分,并据此回答食堂是否需要进行内部整顿.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知二次函数y=f(x)的图象过坐标原点,其导函数f′(x)=6x﹣2,数列{an}前n项和为Sn , 点(n,Sn)(n∈N*)均在y=f(x)的图象上.
(1)求数列{an}的通项公式;
(2)设 ![]() ,Tn是数列{bn}的前n项和,求当
,Tn是数列{bn}的前n项和,求当 ![]() 对所有n∈N*都成立m取值范围.
对所有n∈N*都成立m取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】2014年7月16日,中国互联网络信息中心发布《第三十四次中国互联网发展状况报告》,报告显示:我国网络购物用户已达![]() 亿.为了了解网购者一次性购物金额情况,某统计部门随机抽查了6月1日这一天100名网购者的网购情况,得到如下数据统计表.已知网购金额在2000元以上(不含2000元)的频率为
亿.为了了解网购者一次性购物金额情况,某统计部门随机抽查了6月1日这一天100名网购者的网购情况,得到如下数据统计表.已知网购金额在2000元以上(不含2000元)的频率为![]() .
.

(Ⅰ)确定![]() ,
, ![]() ,
, ![]() ,
, ![]() 的值;
的值;
(Ⅱ)为进一步了解网购金额的多少是否与网龄有关,对这100名网购者调查显示:购物金额在2000元以上的网购者中网龄3年以上的有35人,购物金额在2000元以下(含2000元)的网购者中网龄不足3年的有20人.
①请将列联表补充完整;
网龄3年以上 | 网龄不足3年 | 合计 | |
购物金额在2000元以上 | 35 | ||
购物金额在2000元以下 | 20 | ||
合计 | 100 |
②并据此列联表判断,是否有![]() %的把握认为网购金额超过2000元与网龄在三年以上有关?
%的把握认为网购金额超过2000元与网龄在三年以上有关?
参考数据:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(参考公式:  ,其中
,其中![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com