
【题目】已知椭圆C中心在原点,焦点在坐标轴上,且该椭圆经过点( ![]() ,
, ![]() )和点
)和点 ![]() .求
.求
(1)椭圆C的方程;
(2)P,Q,M,N四点在椭圆C上,F1为负半轴上的焦点,直线PQ,MN都过F1且 ![]() ,求四边形PMQN的面积最小值和最大值.
,求四边形PMQN的面积最小值和最大值.
【答案】
(1)解:由题意,设椭圆的方程为mx2+ny2=1(m,n>0,m≠n),
代入点( ![]() ,
, ![]() )和点
)和点 ![]() ,可得
,可得
![]() m+
m+ ![]() n=1,
n=1, ![]() m+n=1,
m+n=1,
解得m=1,n= ![]() ,
,
即有椭圆方程为x2+ ![]() =1
=1
(2)解:由 ![]() ,可得直线PQ,MN垂直.
,可得直线PQ,MN垂直.
(ⅰ)若MN与PQ中一条斜率不存在,另一条斜率为0,
则四边形PMQN的面积S= ![]() 2a
2a ![]() =2b2=2;
=2b2=2;
(ⅱ)若PQ与NM的斜率均存在,
设PQ:y=kx+1与椭圆方程联立 ![]()
消去y可得(2+k2)x+2kx﹣1=0,则△=8(k2+1)>0,
设P(x1,y1),Q(x2,y2),
则x1+x2=﹣ ![]() ,x1x2=﹣
,x1x2=﹣ ![]() ,
,
∴|PQ|= ![]() |x1﹣x2|=
|x1﹣x2|= ![]()
![]() =2
=2 ![]()
![]() ;
;
同理可得|MN|=2 ![]()
![]() .
.
∴S= ![]() |PQ||MN|=4
|PQ||MN|=4 ![]() =
= 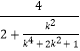 =
= 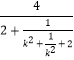 ,
,
由k2+ ![]() ≥2,得
≥2,得 ![]() ≤S<2.
≤S<2.
由(ⅰ)(ⅱ)知,Smin= ![]() ,Smax=2
,Smax=2
【解析】(1)由题意,设椭圆的方程为mx2+ny2=1(m,n>0,m≠n),代入两点的坐标,建立方程组,从而可求椭圆的几何量,即可求椭圆C的方程;(2)分斜率存在与存在分别讨论,利用直线与椭圆联立,根据韦达定理及弦长公式,确定面积的表达式,运用基本不等式可得最值,即可求得结论.


 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:高中数学 来源: 题型:
【题目】如图,现要在边长为100m的正方形ABCD内建一个交通“环岛”.以正方形的四个顶点为圆心在四个角分别建半径为xm(x不小于9)的扇形花坛,以正方形的中心为圆心建一个半径为 ![]() m的圆形草地.为了保证道路畅通,岛口宽不小于60m,绕岛行驶的路宽均小于10m.
m的圆形草地.为了保证道路畅通,岛口宽不小于60m,绕岛行驶的路宽均小于10m. 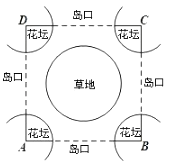
(1)求x的取值范围;(运算中 ![]() 取1.4)
取1.4)
(2)若中间草地的造价为a元/m2 , 四个花坛的造价为 ![]() 元/m2 , 其余区域的造价为
元/m2 , 其余区域的造价为 ![]() 元/m2 , 当x取何值时,可使“环岛”的整体造价最低?
元/m2 , 当x取何值时,可使“环岛”的整体造价最低?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,PA⊥底面ABCD,AD⊥AB,AB∥DC,AD=DC=AP=2,AB=1,点E为棱PC的中点. 
(1)证明:BE⊥DC;
(2)求直线BE与平面PBD所成角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知二次函数y=f(x)的图象过坐标原点,其导函数f′(x)=6x﹣2,数列{an}前n项和为Sn , 点(n,Sn)(n∈N*)均在y=f(x)的图象上.
(1)求数列{an}的通项公式;
(2)设 ![]() ,Tn是数列{bn}的前n项和,求当
,Tn是数列{bn}的前n项和,求当 ![]() 对所有n∈N*都成立m取值范围.
对所有n∈N*都成立m取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
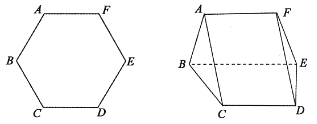
【题目】如图,将边长为2的正六边形ABCDEF沿对角线BE翻折,连接AC、FD,形成如图所示的多面体,且![]() ,(1)证明:平面ABEF
,(1)证明:平面ABEF![]() 平面BCDE; (2)求DE与平面ABC所成角的正弦值。
平面BCDE; (2)求DE与平面ABC所成角的正弦值。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
, ![]() .
.
(1)若曲线![]() 与
与![]() 在公共点
在公共点![]() 处有相同的切线,求实数
处有相同的切线,求实数![]() 的值;
的值;
(2)当![]() 时,若曲线
时,若曲线![]() 与
与![]() 在公共点
在公共点![]() 处有相同的切线,求证:点
处有相同的切线,求证:点![]() 唯一;
唯一;
(3)若![]() ,
, ![]() ,且曲线
,且曲线![]() 与
与![]() 总存在公切线,求:正实数
总存在公切线,求:正实数![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
, ![]() .
.
(1)当![]() 时,求函数
时,求函数![]() 的最小值;
的最小值;
(2)当![]() 时,讨论函数
时,讨论函数![]() 的单调性;
的单调性;
(3)是否存在实数![]() ,对任意的
,对任意的![]() ,
, ![]() ,且
,且![]() ,有
,有![]() 恒成立,若存在求出
恒成立,若存在求出![]() 的取值范围,若不存在,说明理由.
的取值范围,若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com