【题目】已知 ， 的夹角为120°，且| |=4，| |=2．求：
（1）（ ﹣2 ）（ + ）；
（2）|3 ﹣4 |．

【题目】如图所示，某小区为美化环境，准备在小区内草坪的一侧修建一条直路，另一侧修建一条休闲大道，它的前一段是函数， 的一部分，后一段是函数（， ），时的图象，图象的最高点为， ，垂足为.

（1）求函数的解析式；

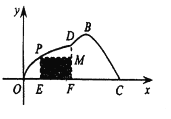
（2）若在草坪内修建如图所示的儿童游乐园PMFE，问点落在曲线上何处时，儿童乐园的面积最大？

【题目】已知函数

（1）若是的极值点，求的极大值；

（2）求实数的范围，使得恒成立.

【题目】（本小题满分12分）已知函数．

（Ⅰ）当时，求曲线在点处的切线方程；

（Ⅱ）求函数的极值．

【题目】从一批有10个合格品与3个次品的产品中，一件一件地抽取产品，设各个产品被抽取到的可能性相同．在下列三种情况下，分别求出直到取出合格品为止时所需抽取次数x的分布列．
（1）每次取出的产品都不放回此批产品中；
（2）每次取出的产品都立即放回此批产品中，然后再取出一件产品；
（3）每次取出一件产品后总以一件合格品放回此批产品中．

【题目】如图所示，已知长方体ABCD﹣A1B1C1D1中，AB=BC=2，AA1=4，E是棱CC1上的点，且BE⊥B1C．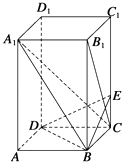
（1）求CE的长；
（2）求证：A1C⊥平面BED；
（3）求A1B与平面BDE夹角的正弦值．

【题目】已知函数， ，函数的图象在点处的切线平行于轴．

（1）确定与的关系；

（2）若，试讨论函数的单调性．

【题目】两千多年前，古希腊毕达哥拉斯学派的数学家曾经在沙滩上研究数学问题．他们在沙滩上画点或用小石子表示数，按照点或小石子能排列的形状对数进行分类．如下图中实心点的个数5，9，14，20，…为梯形数．根据图形的构成，记此数列的第2013项为a2013 ， 则a2013﹣5=（ ）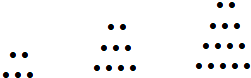
A.2019×2013
B.2019×2012
C.1006×2013
D.2019×1006

【题目】下列结论正确的是（ ）
A.各个面都是三角形的几何体是三棱锥
B.一平面截一棱锥得到一个棱锥和一个棱台
C.棱锥的侧棱长与底面多边形的边长相等，则该棱锥可能是正六棱锥
D.圆锥的顶点与底面圆周上的任意一点的连线都是母线

【题目】综合题。
（1）现有5名男生和3名女生．若从中选5人，且要求女生只有2名，站成一排，共有多少种不同的排法？
（2）从{﹣3，﹣2，﹣1，0，1，2，3，4}中任选三个不同元素作为二次函数y=ax2+bx+c的系数，问能组成多少条经过原点且顶点在第一象限或第三象限的抛物线？
（3）已知（ +2x）n ， 若展开式中第5项、第6项与第7项的二项式系数成等差数列，求展开式中二项式系数最大项的系数．